Figure 10-59 shows an arrangement of 15 identical disks that have been glued together in a rod-like shape of length L = 1.0000 m and (total) mass M = 100.0 mg. The disks are uniform, and the disk arrangement can rotate about a perpendicular axis through its central disk at point O. (a) What is the rotational inertia of the arrangement about that axis? (b) If we approximated the arrangement as being a uniform rod of mass M and length L, what percentage error would we make in using the formula in Table 10-2e to calculate the rotational inertia?
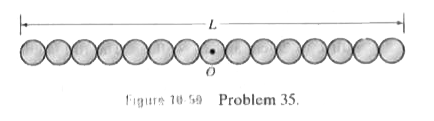
(a) 8.352×10−3kg⋅m2, (b) 0.22%
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
43 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
7 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
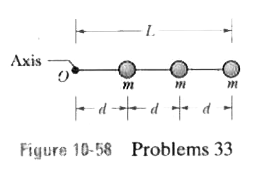
Figure 10-58 shows three 0.0100 kg particles that have been glued to a rod of length L = 8.00 cm and negligible mass. The assembly can rotate around a perpendicular axis through point O at the left end. If we remove one particle (that is, 33% of the mass), by what percentage does the rotational inertia of the assembly around the rotation axis decrease when that removed particle is (a) the inner-most one and (b) the outermost one?
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View Solution
Knowledge Check
The moment of inertia of a thin uniform rod of mass M and length l about an axis perpendicular to the rod through its centre is I. The moment of inertia of the rod through its end point is
AI4BI2C2ID4IThe moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about an axis perpendicular to rod through its end point is
AI4BI2C2ID4IThree rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be
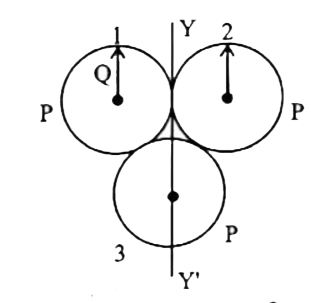 A72PQ2B27PQ2C25PQ2D52PQ2
A72PQ2B27PQ2C25PQ2D52PQ2

A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionFigure shows a thin, uniform rod of mass M and length L, on an x axis with the origin at the rod's center.
(a) What is the rotational inertia of the rod about the perpendicular rotation axis through the center?
(b) What is the rod's rotational inertia I about a new rotation axis that is perpendicular to the rod and through the left end?
View SolutionSeven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is :

View SolutionThe M.I. of thin uniform rod of mass 'M' and length 'l' about an axis passing through its centre and perpendicular to its length is
View Solution
