The U-tube in Fig contains two liquids in static equilibrium : Water of density ρw=(998kg/m3) is in the right arm , and oil of unknown density ρ , is in the left . Measurement gives l = 135 mm and d = 12.3 mm .what is the density of the oil ?
To find the density of the oil in the U-tube, we can use the principle of hydrostatic equilibrium. The pressures at the same horizontal level in both arms of the U-tube must be equal.
1. Identify the given values:
- Density of water, ρw=998kg/m3
- Length of water column, L=135mm=0.135m
- Length of oil column, d=12.3mm=0.0123m
2. Set up the pressure equations:
- The pressure at the interface in the left arm (oil) can be expressed as:
PA=P0+ρ⋅g⋅(L+d)
- The pressure at the interface in the right arm (water) can be expressed as:
PB=P0+ρw⋅g⋅L
3. Equate the pressures:
Since both pressures at the interface must be equal, we can set PA=PB:
P0+ρ⋅g⋅(L+d)=P0+ρw⋅g⋅L
4. Cancel out common terms:
- Cancel P0 and g from both sides:
ρ⋅(L+d)=ρw⋅L
5. Solve for the density of oil, ρ:
ρ=ρw⋅LL+d
- Substitute the known values:
ρ=998kg/m3⋅0.135m0.135m+0.0123m
6. Calculate the denominator:
L+d=0.135m+0.0123m=0.1473m
7. Calculate the density of oil:
ρ=998⋅0.1350.1473≈914.6kg/m3
Final Answer:
The density of the oil is approximately 914.6kg/m3.
---
- Density of water, ρw=998kg/m3
- Length of water column, L=135mm=0.135m
- Length of oil column, d=12.3mm=0.0123m
- The pressure at the interface in the left arm (oil) can be expressed as:
PA=P0+ρ⋅g⋅(L+d)
- The pressure at the interface in the right arm (water) can be expressed as:
PB=P0+ρw⋅g⋅L
Since both pressures at the interface must be equal, we can set PA=PB:
P0+ρ⋅g⋅(L+d)=P0+ρw⋅g⋅L
- Cancel P0 and g from both sides:
ρ⋅(L+d)=ρw⋅L
ρ=ρw⋅LL+d
- Substitute the known values:
ρ=998kg/m3⋅0.135m0.135m+0.0123m
L+d=0.135m+0.0123m=0.1473m
ρ=998⋅0.1350.1473≈914.6kg/m3
The density of the oil is approximately 914.6kg/m3.
Topper's Solved these Questions
- FLUIDSBook:RESNICK AND HALLIDAYChapter:FLUIDSExercise:SAMPLE PROBLEM 14.04
Explore 1 Video
- FLUIDSBook:RESNICK AND HALLIDAYChapter:FLUIDSExercise:SAMPLE PROBLEM 14.05
Explore 1 Video
- FLUIDSBook:RESNICK AND HALLIDAYChapter:FLUIDSExercise:SAMPLE PROBLEM 14.02
Explore 1 Video
- ELECTROMAGNETIC WAVES Book:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC WAVES Exercise:PRACTICE QUESTIONS (Integer Type)
Explore 3 Videos
- FORCE AND MOTION - I Book:RESNICK AND HALLIDAYChapter:FORCE AND MOTION - I Exercise:PRACTICE QUESTIONS (Integer Type)
Explore 3 Videos
Similar Questions
A body weighs W1 in a liquid of density ρ1 and W2 in a liquid of density ρ2. What is the weight of body in a liquid of density ρ3?
View SolutionA U-tube contains water in its lower part. Then 32 cm of kerosene of relative density 0.8 is poured into one limb and a vegetable oil of reative density 0.65 is poured into the other. The water level in the kerosene oil side is 5 cm lower that in the other . what is the height of the column of vegtable oil ?\
View Solution
Knowledge Check
The U-tube in figure contains two different liquids in static equilibrium, water in the right arm and oil of unknown density ρx in the left. If/=135 mm and d=15 mm. Density of the oil is
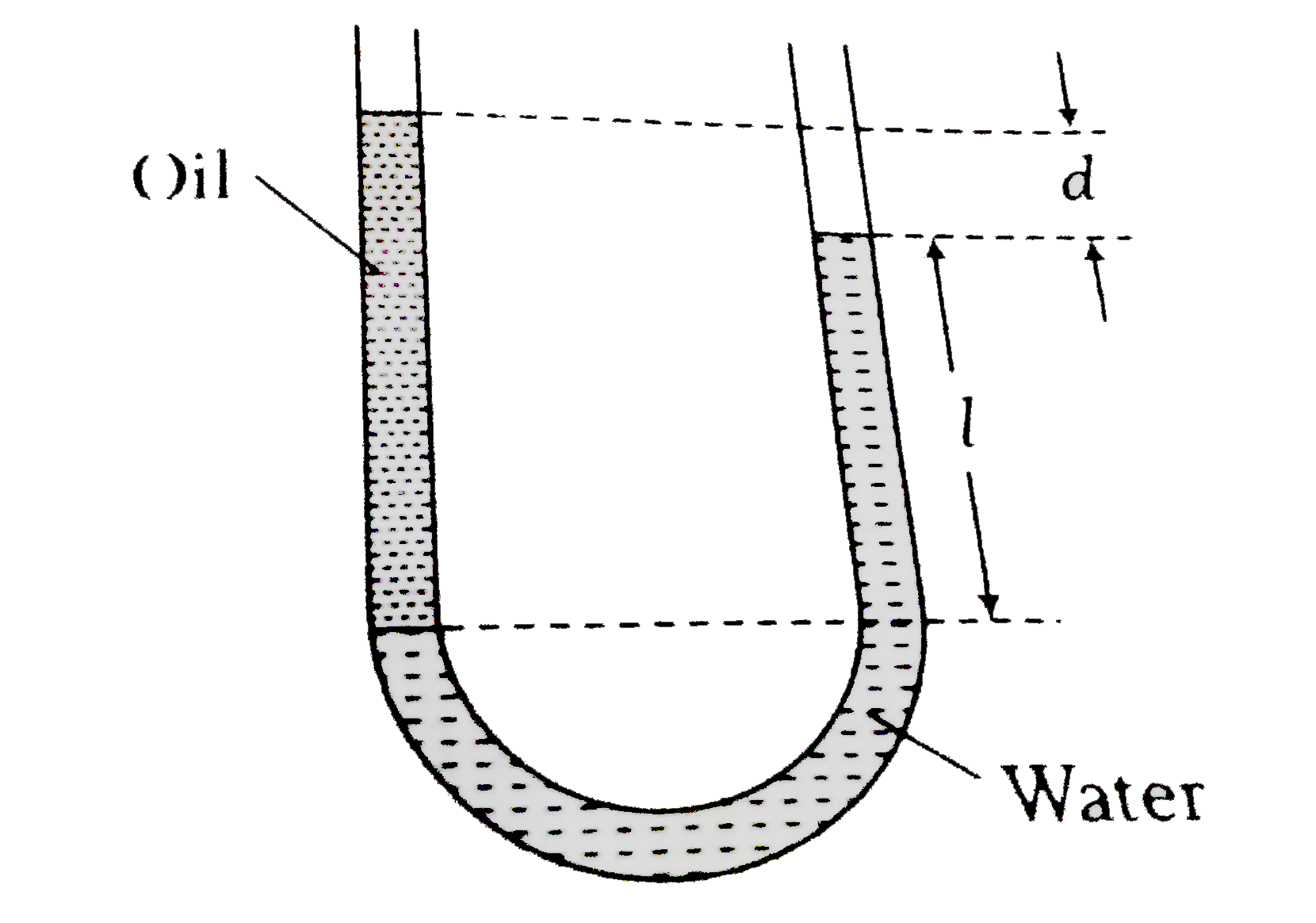 A1000kgm3B920kgm3C895kgm3D900kgm3
A1000kgm3B920kgm3C895kgm3D900kgm3What is the mass of one litre of cottonseed oil of density 926kg/m3
A926 kgB92.6 kgC0.926 kgD9260 kgA liquid X of density 3.36g/cm3 poured in a U-tube which contains Hg. Another liquid Y is poured in left arm with heght 8 cm upper levels of X and Y are same. What is density of Y?
A0.8g/cB1.2g/cC1.4g/cD1.6g/c
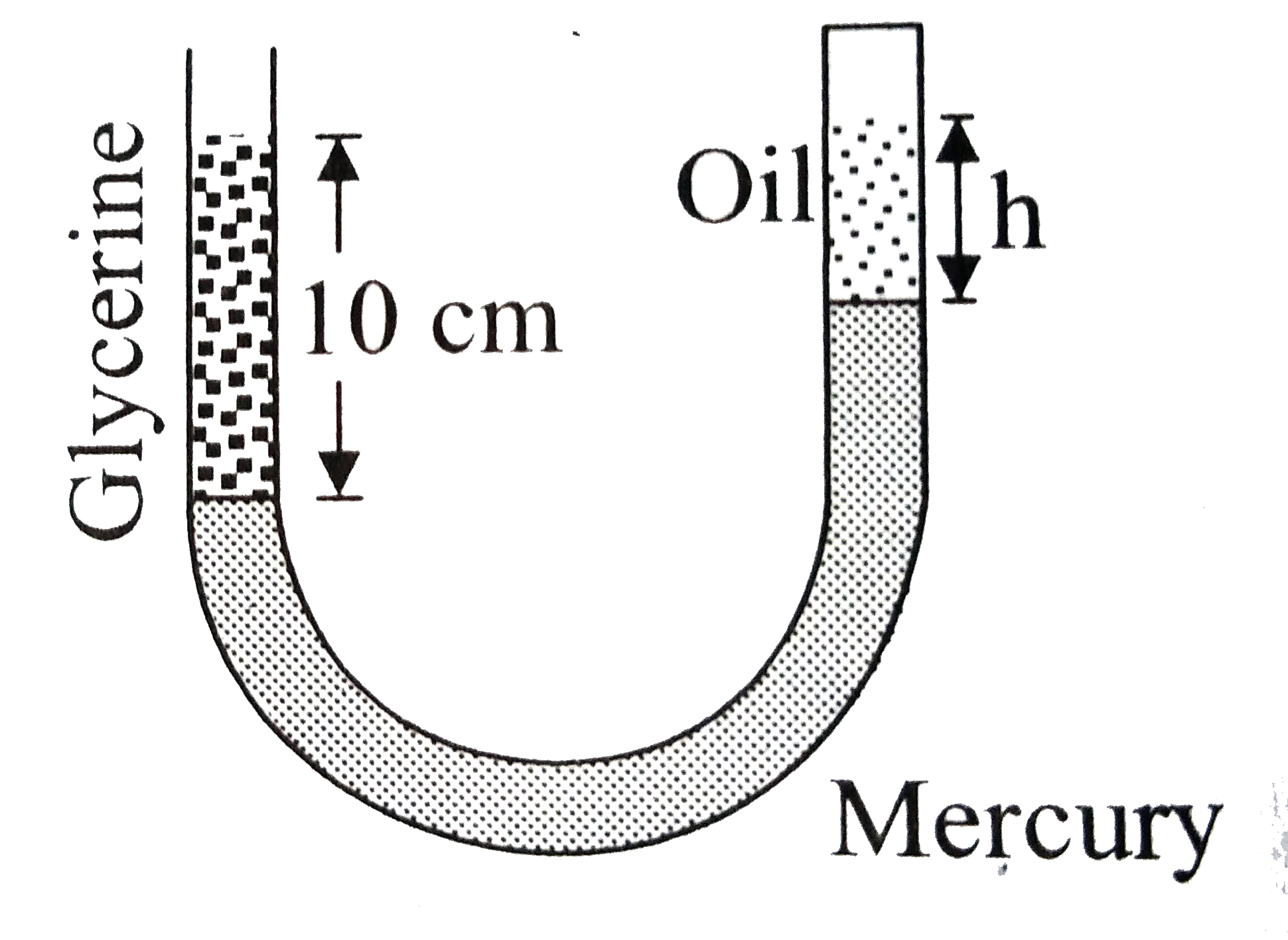
A vertical U-tube of uniform inner cross section contains mercury in both sides of its arms. A glycerin (density =1.3g/cm3) column of length 10 cm is introduced into one of its arms. Oil of density 0.8 gm/cm3 is poured into the other arm until the upper surfaces of the oil and glycerin are in the same horizontal level. Find the length of the same horizontal level. Find the length of the oil column, Density of mercury =13.6g/cm3
View SolutionA simple pendulum of length 4.9m is immersed in a liquid of density ρ=0.4kg/m3. Then the time period of pendulum is (density of bob =0.8kg/m3)
View SolutionThe figure represents a U-tube of uniform cross-section filled with two immiscible liquids. One is water with density ρw and the other liquid is of density ρ . The liquid interface lies 2cm above the base. The relation between ρ and ρw is
 .
.
View SolutionA metallic sphere floats in an immiscribe mixture of water (ρw=103kg/m3) and a liquid (ρL=13.5×103) with (1//5)th portion by volume in the liquid and remaning in water. The density of the metal is :
View Solution_E01_173_Q01.png)
In a U-tube if different liquids are filled then we can say that pressure at same level of same liquid is same.
Q. In a U-tube 20 cm of a liquid of density ρ is on left hand side and 10 cm of another liquid of density 1.5 ρ is on right hand side in between them there is a third liquid of density 2ρ what is the value of h.
View Solution
