A metallic sphere floats in an immiscribe mixture of water (ρw=103kg/m3) and a liquid (ρL=13.5×103) with (1//5)th portion by volume in the liquid and remaning in water. The density of the metal is :
4.5×103kg/m3
4.0×103kg/m3
3.5×103kg/m3
1.9×103kg/m3
The correct Answer is:C
Step by step video, text & image solution for A metallic sphere floats in an immiscribe mixture of water (rho_(w) = 10^(3) kg//m^(3)) and a liquid (rho_(L) = 13.5 xx 10^(3)) with (1//5)th portion by volume in the liquid and remaning in water. The density of the metal is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBook:RESONANCEChapter:FLUID MECHANICSExercise:Exercise- 1 PART - II Section (C)
Explore 6 Videos
- FLUID MECHANICSBook:RESONANCEChapter:FLUID MECHANICSExercise:Exercise- 2 PART - I
Explore 18 Videos
- FLUID MECHANICSBook:RESONANCEChapter:FLUID MECHANICSExercise:Exercise- 1 PART - II Section (A)
Explore 6 Videos
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:Exercise
Explore 52 Videos
- FULL TEST 1Book:RESONANCEChapter:FULL TEST 1Exercise:Exercise
Explore 30 Videos
Similar Questions
A metallic sphere floats in an immiscible mixture of water (ρw=103kg/m3) and a liquid (ρL=13.5×103kg/m3) such that its 45th volume is in water and 15th volume in the liquid. Find the density of metal.
View SolutionA cube of 1 kg is floating at the interface of two liquids of density ρ1=3/4gm/cm3andρ2=2.5gm/cm3 The cube has (3/5)th part in ρ2 and (2/5)th part in ρ1 .Find the density of the cube .

View Solution
Knowledge Check
A metallic sphere floats in immiscible mixture of water (density 103kgm−3) and a liquid (density 8×103kgm−3) such that its (2/3) part is in water and (1/3) part in the liquid. The density of the metal is
A50003kgm−3B100003kgm−3C5000kgm−3D2000kgm−3Two immisible liquids are pured in a U-tube having densities ρ1=1.0×102kg/m2andρ22.0×103kg/m3. Find the ratio of heights (of the liquids above their interface) n1h2
 A3B6C9D12
A3B6C9D12Two liquids of densities 2ρ and ρ having their volumes in the ratio 3:2 are mixed together. Density of the mixture will be
A2ρ3Bρ2C8ρ5D4ρ5
A vessel contains two immiscible liquids of densit ρ1=1000kg/m3 and ρ2=1500kg/m3. A solid block of volume V=103m3 and density d=800kg/m3 is tied to one end of a string and the outer end is tied to the bottom of the vessel as shown in figure.
The block is immersed with two fifths of its volume in the liquid of lower density. The entire system is kept in an elavator which is moving upwards with an acceleration of a=g2. Find the tension in the string. brgt
View SolutionA block of density ρ1 floats in two immiscible liquids of density 4ρ and 2ρ , such that (14)th portion is in liquid of density 4ρ and remaining liquid of density 2ρ ,then ρ1=_________g(cm)3(Given ρ=0.8g(cm)3)
View Solution(i) One end of a uniform glass capillary tube of radius r=0.025 cm is immersed vertically in water to a depth h=1cm. Contact angle is 0∘, surface tension of water is 7.5×10–2N/m, density of water is ρ=103kg/m3 and atmospheric pressure is Po=105N/m2
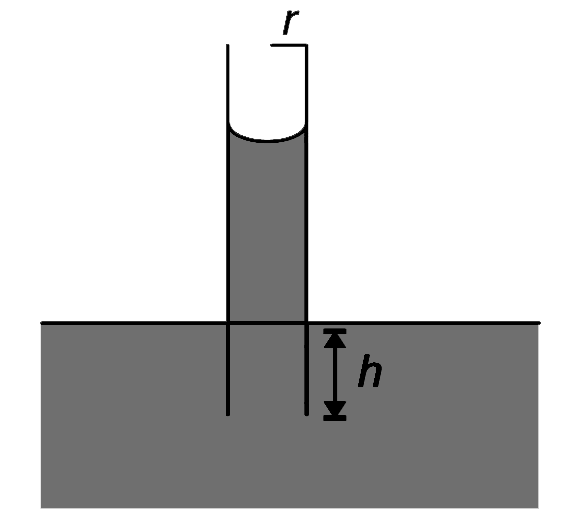
Find the excess pressure to be applied on the water in the capillary tube so that -
(a) The water level in the tube becomes same as that in the vessel.
(b) Is it possible to blow out an air bubble out of the tube by increasing the pressure? (ii) A container contains two immiscible liquids of density ρ1 and ρ2(ρ2>ρ1). A capillary of radius r is inserted in the liquid so that its bottom reaches up to denser liquid and lighter liquid does not enter into the capillary. Denser liquid rises in capillary and attain height equal to h which is also equal to column length of lighter liquid. Assuming zero contact angle find surface tension of the heavier liquid.
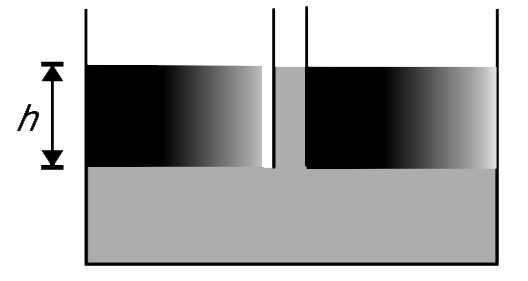
View SolutionA body is floating in water with 3/5th of its volume below the water surface. What will be density of the body?
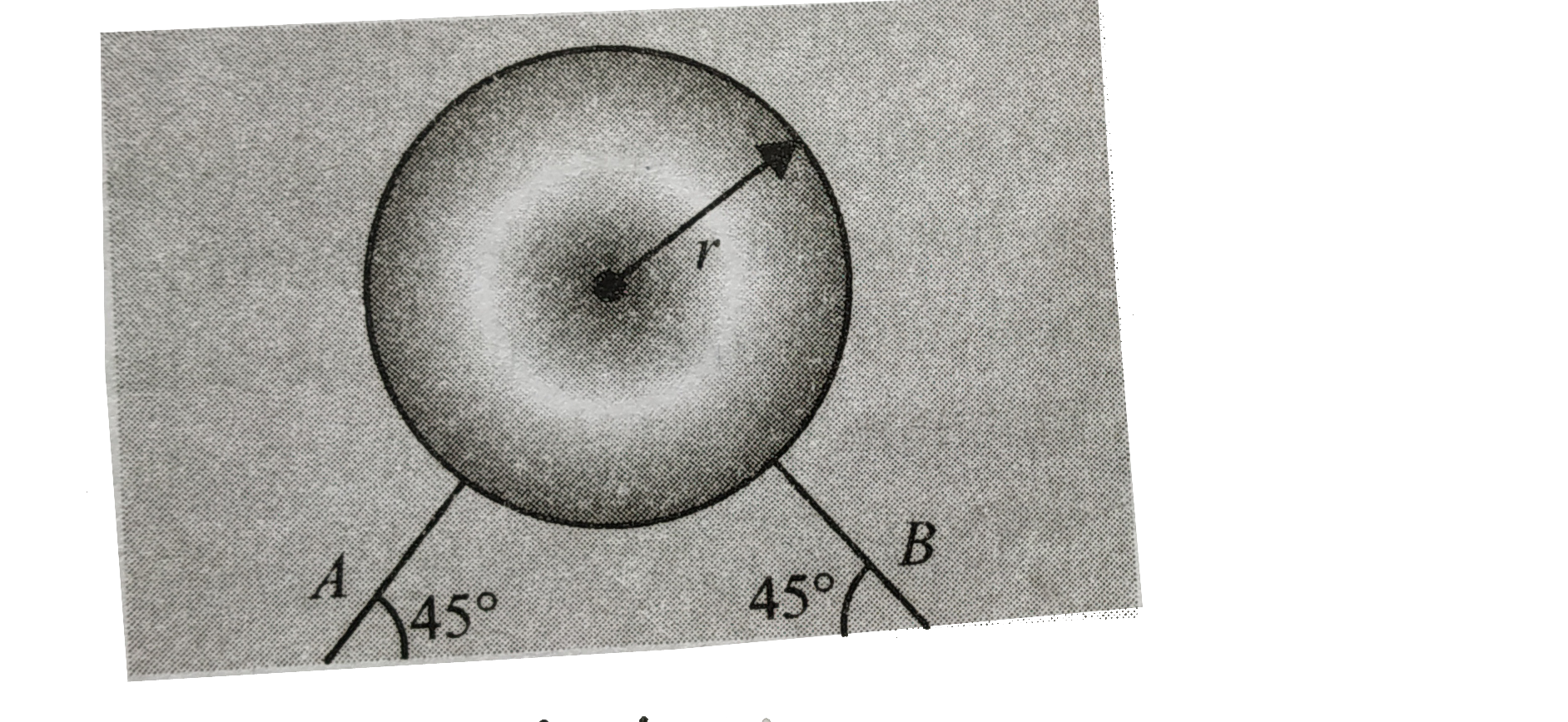
View SolutionA hollow sphere of mass M=50kg and radius r=(340π)1/3m is immersed in a tank of water (density ρw=103kg/m3). The sphere is tied to the bottom of a tank by two wires A and B as shown. Tension in wire A is (g=10m/s2)
View Solution

