Two immisible liquids are pured in a U-tube having densities ρ1=1.0×102kg/m2andρ22.0×103kg/m3. Find the ratio of heights (of the liquids above their interface) n1h2

3
6
9
12
The correct Answer is:A
p0+ρ1gh1=p0+ρ2gh2⇒h1h2=ρ2ρ1=3
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP.No.71
Explore 1 Video
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.71
Explore 10 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Knowledge Check
A narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
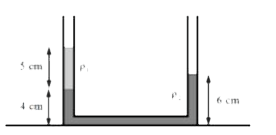 A13B25C12D45
A13B25C12D45Three different liquids are filled in a U-tube as shown in figure. Their densities are ρ1,ρ2 and ρ3 respectively. From the figure we may conclude that
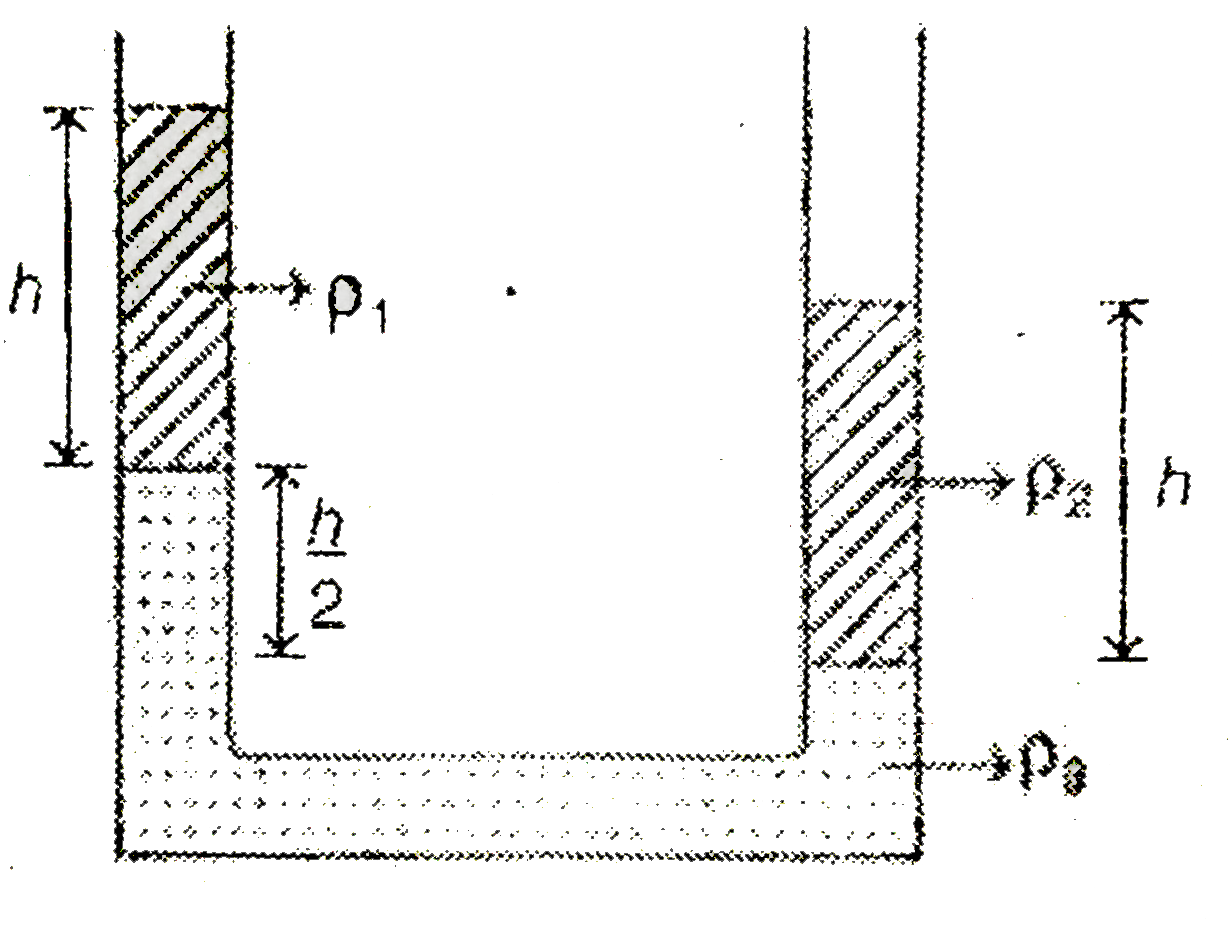 Aρ2>ρ1Bρ1>ρ2Cρ3=2(ρ2−ρ1)Dρ3=ρ2+ρ12
Aρ2>ρ1Bρ1>ρ2Cρ3=2(ρ2−ρ1)Dρ3=ρ2+ρ12A metallic sphere floats in an immiscribe mixture of water (ρw=103kg/m3) and a liquid (ρL=13.5×103) with (1//5)th portion by volume in the liquid and remaning in water. The density of the metal is :
A4.5×103kg/m3B4.0×103kg/m3C3.5×103kg/m3D1.9×103kg/m3
A glass ball of 4.0 mm diameter falls in a glycerine solution (ρ0=1.21×103kg/m3,η=5.02×10−2Pa⋅s). The density of the glass is ρ=2.53×103kg/m3. Find the steady-state speed and the initial acceleration. Make an approximate estimate of the time in which the ball travels during this time.
View SolutionThe speed of sound in a liquid of density 2×103kg/m3 is 1000 m/s. Determine the bulk modulus of elasticity of the liquid.
View SolutionA siphon tube is discharging a liquid of density
900kgm3 as shown in figure. (P0=1.01×105N/m2)

Pressure at point B is
View SolutionA siphon tube is discharging a liquid of density
900kgm3 as shown in figure. (P0=1.01×105N/m2)
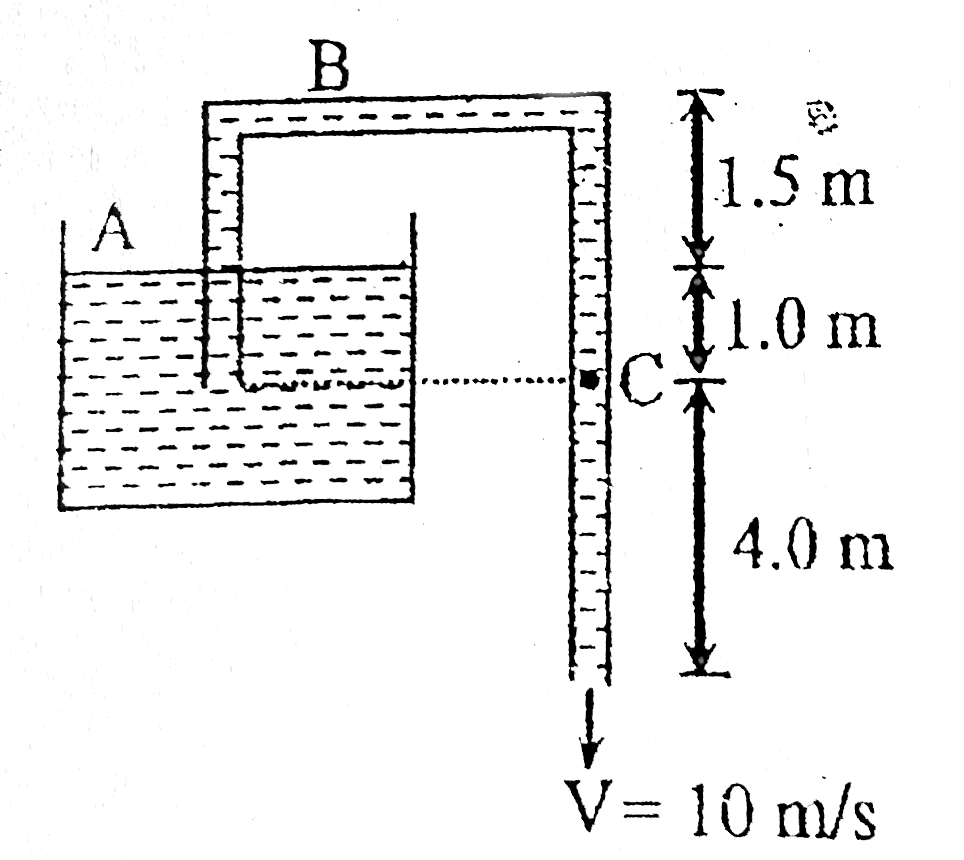
Pressure at point C is
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
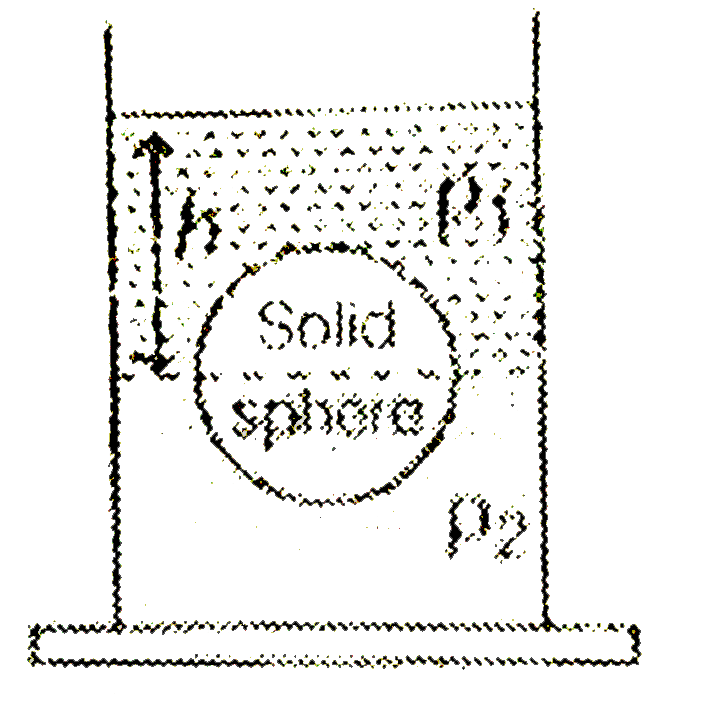
View Solution


