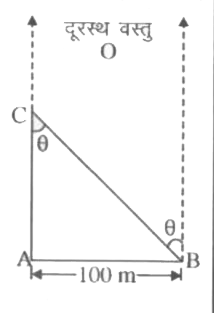
A man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicualr to AC upto B, a distaance of 100m and looks at O and C again. Since O is very distant, the direction of BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle θ=40∘(θis known as parallax). Estimate the distance fo the tower C from his original position A.Solution in Tamil
We have, parallax angle θ=40∘ From fig.2.3. AB=AC tanθ
AC=AB/tanθ = 100m/tan40∘=100m/0.8391=119
Topper's Solved these Questions
- UNITS AND MEASUREMENTBOOK - NCERT TAMILCHAPTER - UNITS AND MEASUREMENTEXERCISE - Exercise (Fill in the blanks)
8 Videos
- UNITS AND MEASUREMENTBOOK - NCERT TAMILCHAPTER - UNITS AND MEASUREMENTEXERCISE - EXERCISE
29 Videos
- THERMODYNAMICS BOOK - NCERT TAMILCHAPTER - THERMODYNAMICS EXERCISE - EXERCISES
10 Videos
- WAVESBOOK - NCERT TAMILCHAPTER - WAVESEXERCISE - EVALUATION(IV. NUMERICAL PROBLEMS)
7 Videos
Similar Questions
Fill in the blanks
(a) The volume of a cube of side 1 cm isk equal to….. m3
(b) the surface area fo a solid cylinder of radius 2.0 cm and height 10.0 cm is equal to …. (mm)2
(c ) A vehical moving with a speed of 18kmh−1 covers ....m in 1s.
(d) The relative density of lead is 11.3. its density is ......g cm−3or.....kgm−3
View SolutionA calorie is a unit of heat or energy and it equals about 4.2J,where1J=1kgm2s−2. Suppose we employ a system of units in which the unit of mass equals αkg, the unit of length equals is βm , the unit of time is γs. Show tthat a calorie has a magnitude 4.2α−1β−1γ2 in terms of the new units.
View SolutionA boiler heats water flowing at the rate of 2,0 litres per minute from 27°C to 77°C. If the boiler operates on a gas burner, the rate of consumption of the fuel if its heat of combustion is 4.0×104J/g , is
View SolutionThe speed of a wave in a certain medium is 900 m/s. If 3000 waves passes over a certain point of the medium in 2 minutes, then compute its wavelength?
View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicualr to AC upto B, a distaance of 100m and looks at O and C again. Since O is very distant, the direction of BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle theta = 40^@ ( theta "is known as parallax"). Estimate the distance fo the tower C from his original position A.
View Solutionएक व्यक्ति अपने पास की किसी मीनार की अपने से दूरी का आकलन करना चाहता है । वह मीनार C के सामने किसी बिंदु A पर खड़ा होता है और AC की सीध में बहुत दूर स्थित किसी बिंदु O को देखता है । फिर वह, AC के लंबवत 100 m दूर स्थित बिंदु B तक चलता है और वहाँ से O एवं C को फिर देखता है । क्योंकि O बहुत अधिक दूरी पर है , BO एवं AO की दिशाएँ व्यावहारिक रूप में एक ही हैं, लेकिन वह पाता है कि C की दृष्टि रेखा मूल दृष्टि रेखा के सापेक्ष θ=40∘ पर घूम गई है (θ को लम्बन कहा जाता है ) उसकी मूल स्थिति A से मीनार C की दूरी का आकलन कीजिए ।
View Solutionएक निकट दृष्टि दोष वाले मनुष्य का दूर बिन्दु आँख से उसके सामने 80 सेमी पर है। अति दूर की वस्तुओं को स्पष्ट देखने के लिए आवश्यक लेंस की क्षमता क्या होगी?
View Solutionएक व्यक्ति अपने पास की किसी मीनार की अपने से दूरी आकलन करना चाहता है। वह मीनार C के सामने किसी बिंदु A पर खड़ा होता है और AC की सीध में बहुत दूर स्थित किसी बिंदु O को देखता है। फिर वह AC के लंबवत 100 m दूर स्थित बिंदु B तक चलता है। और वहाँ से O एवं C को फिर देखता है। क्योंकि O बहुत अधिक दूरी पर है, BO एवं AO की दिशाएँ व्यावहारिक रूप में एक ही हैं, लेकिन वह पता है कि C की दृष्टि रेखा मूल दृष्टि रेखा के सापेक्ष θ=40∘ पर घूम गई है। (θ को लंबवत कहा जाता है ) उसकी मूल स्थिति A से मीनार C की दूरी का आकलन कीजिए।
View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant , the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle θ=40∘ (θ is known as 'Parallax') estimate the distance of the tower C from his original position A.
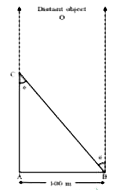
View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant , the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle theta = 40^(@) ( theta is known as 'Parallax') estimate the distance of the tower C from his original position A.
View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant, the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle = 40∘ (θ is known as 'parallax') estimate the distance of the tower C from his original position A.

View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant, the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle = 40∘ (θ is known as 'parallax') estimate the distance of the tower C from his original position A.

View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicualr to AC upto B, a distaance of 100m and looks at O and C again. Since O is very distant, the direction of BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle θ=40∘(θ is known as parallax). Estimate the distance fo the tower C from his original position A.
View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in fron of the tower C and spots a very distant objct O in line with AC. He then walks pependicular to AC up to B, a distance of 100 m and look at O and C again. Since O is very distant the direction BO is practivally the same as AO, but he finds the line of slight by of C shifted fro the original line of slight by an angle θ=30∘(θ is known as parallax) estimate the distance of the tower C from his original position A.
View SolutionA flag staff of the height (a-b) stands on the top of a tower subtends the same angle at the point on the horizontal plalne through the foot of the tower which are at distant a and b from the tower. The height of the tower is
View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant, the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle = 40∘ (θ is known as 'parallax') estimate the distance of the tower C from his original position A.

View Solution
