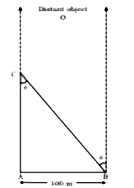
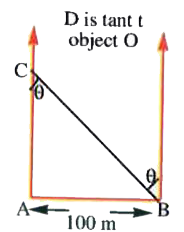
A man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant , the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle θ=40∘ (θ is known as 'Parallax') estimate the distance of the tower C from his original position A.
 Solution in Kannada
Solution in Kannada
We have, parallax angle θ=40∘ From fig.2.3. AB=AC tanθ
AC=AB/tanθ = 100m/tan40∘=100m/0.8391=119
Similar Questions
A man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant, the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle = 40∘ (θ is known as 'parallax') estimate the distance of the tower C from his original position A.
View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicualr to AC upto B, a distaance of 100m and looks at O and C again. Since O is very distant, the direction of BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle θ=40∘(θ is known as parallax). Estimate the distance fo the tower C from his original position A.
View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in fron of the tower C and spots a very distant objct O in line with AC. He then walks pependicular to AC up to B, a distance of 100 m and look at O and C again. Since O is very distant the direction BO is practivally the same as AO, but he finds the line of slight by of C shifted fro the original line of slight by an angle θ=30∘(θ is known as parallax) estimate the distance of the tower C from his original position A.
View Solutionमीनार के आधार से क्षैतिज रेखा में स्थित किसी बिंदु से मीनार के शिखर का उन्नयन कोण 30∘ देखा गया । जब प्रेक्षक मीनार की ओर 100 मी. चलता है तो वह पाता है कि शिखर का उन्नयन कोण 60∘ हो गया है । मीनार की ऊँचाई और प्रथम स्थिति से मीनार की दूरी ज्ञात कीजिए ।
View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant, the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle = 40∘ (θ is known as 'parallax') estimate the distance of the tower C from his original position A.

View SolutionA man wishes to estimate the distance of a nearby tower from him. He stand at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicular to AC up to B, a distant, the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by n angleθ=40∘(θ is known as 'parallax').Estimate the distance of the tower C from the original position A.
View SolutionA man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m and looks at O and C again. Since O is very distant, the direction BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle theta=40^(@) ( theta is known as parallax) estimate the distance of the tower C from his original position A.
View SolutionAt a very distant distance the shape of the wave-front is ...............
View Solution