किसी टावर के पाद से 160 मी . दूर स्थित बिंदु से टावर का उन्नयन कोंढ टावर के पाद की ओर 100 मी . दूरी चलने पर दो गुना हो जाता है । टावर की ऊंचाई ज्ञात करे ।
80 m
100 m
160 m
200 m
The correct Answer is:A
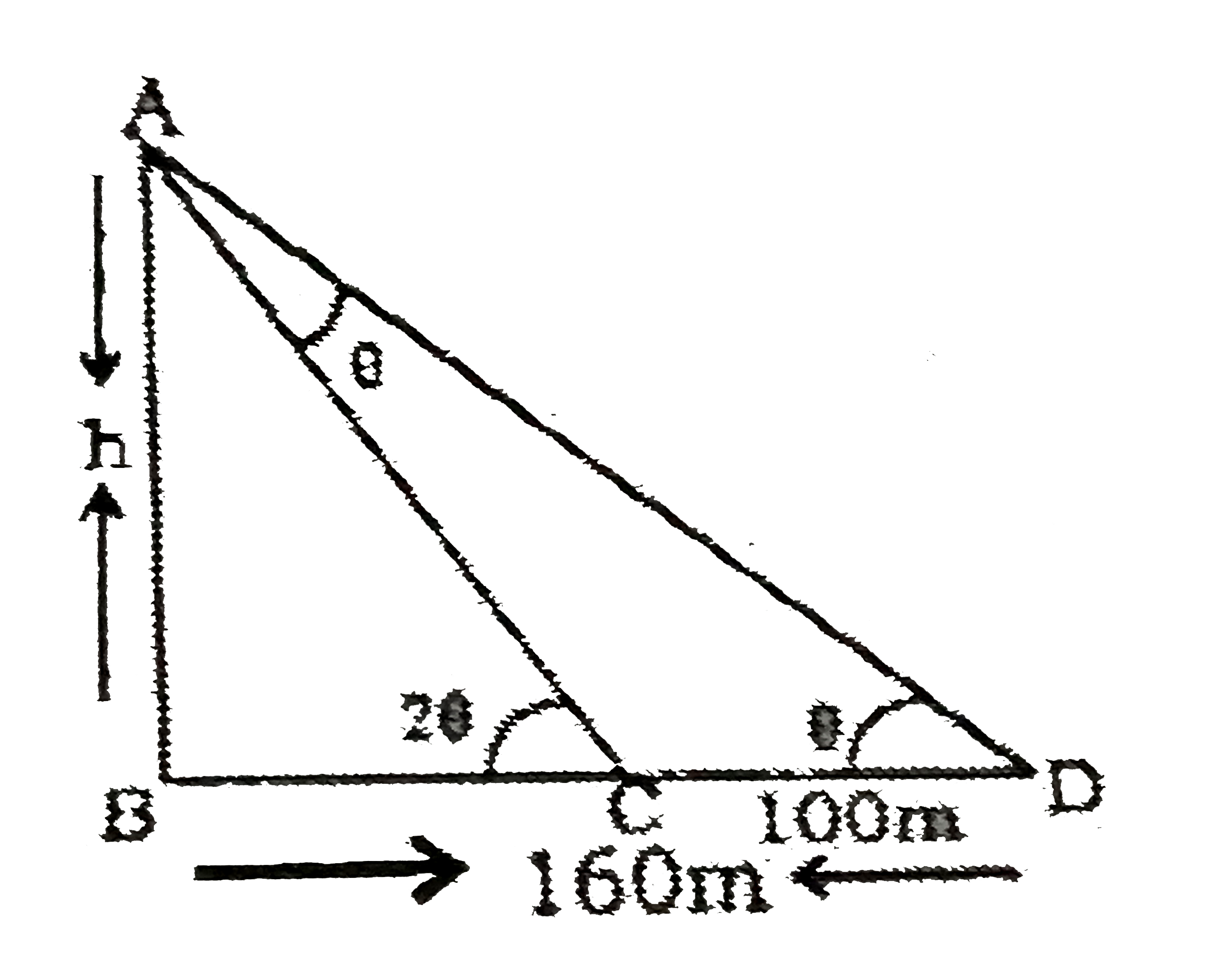
BD=160m
In △ACD
exter. ∠ACB=∠CAD+∠ADC
2θ=∠CAD+θ
∠CAD=θ
∴AC=CD
AC=100 m
In △ABC
AC=100 m
BC=160-100 =60 m
Then AB=80 m (By pythagoras theorem)
Topper's Solved these Questions
Similar Questions
भुवनेश ने 45∘ के स्थान पर 45∘'27 का कोण बनाया । प्रतिशत त्रुटि ज्ञात करे ।
View Solutionदो संख्याओं का म0स0 तथा ल0 स0 क्रमशः 15 तथा 300 है। यदि एक संख्या 60 है तो दूसरी संख्या ज्ञात करें?
View Solutionकिसी त्रिभुज के शीर्षो से समान दूरी पर स्तिथ बिंदु का नाम लिखि।
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसकी x-अक्ष से दूरी उसकी y-अक्ष से दूरी की तीन गुनी है ।
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसकी बिंदु (1, 2) से दूरी उसकी y-अक्ष से दूरी की दो गुनी है ।
View Solutionएक 13 मीटर लम्बी सीढ़ी दीवार के सहारे झुकी हुई है। सीढ़ी के पाद को 1.5 मी./से. की दर से जमीन के सारे दीवार से दूर खींचा जाता है। सीढ़ी तथा जमीन के मध्य का कोण किस गति से परिवर्तित हो रहा है जबकि सीढ़ का पावि दीवार से 12 मीटर दूर हो ।
View Solutionवृत्त के बाहर स्थित बिंदु से खींची गई स्पर्श रेखाओं की संख्या हो सकती है:
View Solutionपरवलय y2=4ax की स्पर्श रेखा पर नाभि से डाले गये लम्ब के पाद का बिन्दुपथ है
View Solutionबिंदु (3,4,5) से समतल x+y+z=9 पर डाले गए लम्ब का पाद बिंदु होगा
View Solutionकिसी बेलन का अर्धव्यास 2 मी/से की दर से बढ़ता है और ऊँचाई 3 मी/से की दर से घटती है। जब उसकी ऊँचाई 5 मी और अर्धव्यास 3 मी हो, तो बेलन के आयतन के परिवर्तन की दर होगी
View Solutionबिंदु P की बिंदु (4,3) से दूरी √10 है। बिंदु P के निर्देशांक ज्ञात कीजिए यदि इस की कोटि भुज से दुगुनी हो।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View Solutionसरल रेखाएँ|एक बिन्दु की रेखा से दूरी#!#दो समांतर रेखाओ के बीच की दूरी#!#प्रश्नो पर चर्चा
View Solutionबिंदु L बिंदु P(3,4,5) से xz तल पर खींचे गए लंब का पाद बिंदु है | बिंदु L के निर्देशांक है
View SolutionFrom a point P, the angle of elevation of a tower is such that its tangent is 3/4. On walking 560 meters towards the tower the tangent of the angle of the elevation of the tower becomes 4/3. What is the height (in meters) of the tower?
एक बिंदु P से, एक टावर की ऊँचाई का कोण ऐसा है कि इसकी स्पर्शरेखा 3/4 है। टॉवर को ओर 560 मीटर चलने पर टॉवर के ऊंचाई के कोण के स्पर्शरेखा 4/3 हो जाती है। मीनार की ऊँचाई (मीटर में) कितनी है?
View Solution
