Lines $5 x + 12 y - 10 = 0$ and $5 x - 12 y - 40 = 0$ touch a circle C1 of diameter 6. If the centre of C1, lies in the first quadrant then the equation of the circle C2, which is concentric with C1, and cuts intercepts of length 8 on these lines is

Video Solution

Text Solution

Verified by Experts

Since, $5 x + 12 y - 10 = 0 and 5 x - 12 y - 40 = 0$ are both perpendicular tangents to the circle $C_{1}$ .
$∴$ OABC forms a square.
Let the centre coordinates be ((h, k), where,
$O C = O A = 3 and O B = 6 \sqrt{2}$
$\Rightarrow \frac{| 5 h + 12 k - 10 |}{13} = 3 and \frac{| 5 h + 12 k - 40 |}{13} = 3$

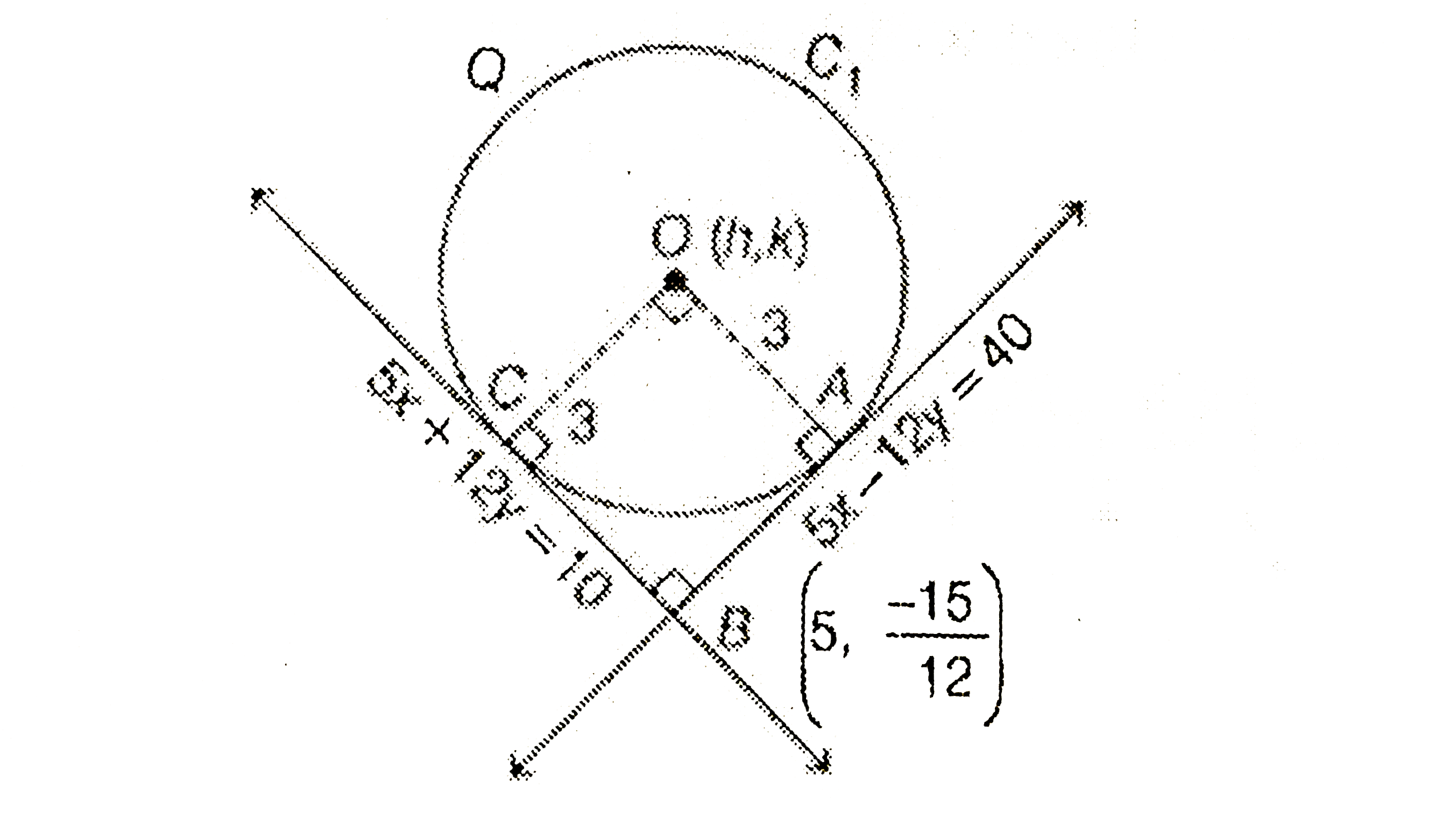
$\Rightarrow 5 h + 12 k - 10 = \pm 39 and 5 h - 12 k - 40 = \pm 39$ on solving above equations. The coordinates which lie in I quadrant are (5, 2).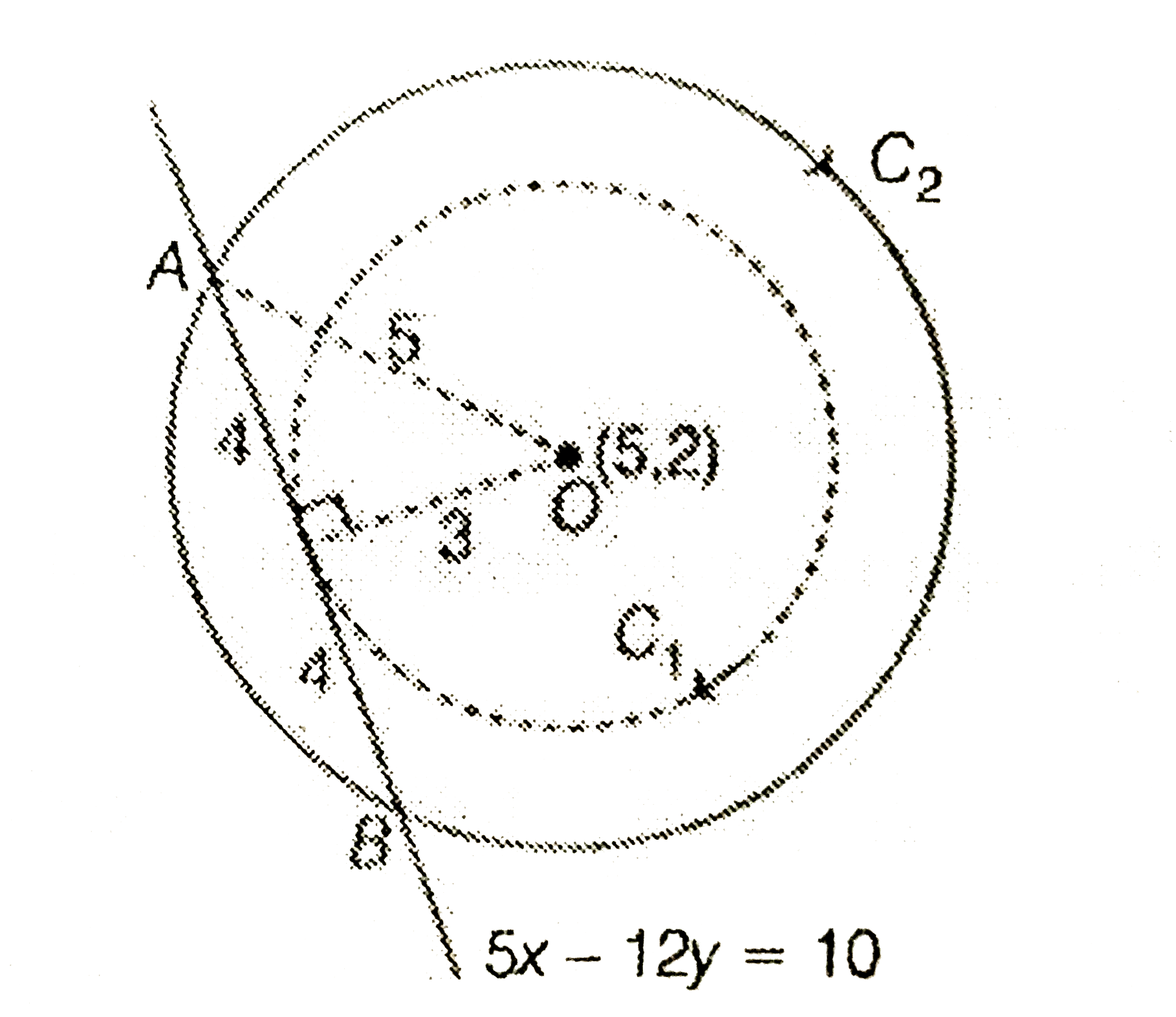
$∴$ Centre for $C_{1} (5, 2)$
To obtain equation of circle concentric with $C_{1}$ and making an intercept of length 8 on 5x + 12y = 10 and 5x - 12y = 40 $∴$ Required equation of circle $C_{2}$ has centre (5, 2) and radius 5 is ${(x - 5)}^{2} + {(y - 2)}^{2} = 5^{2}$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Radius of the circle with centre (3,1) and cutting a chord of length 6 on the line $2 x + 5 y + 18 = 0$ is
A6
B7
C $\sqrt{38}$
D $2 \sqrt{5}$

IIT JEE PREVIOUS YEAR-CIRCLE-Topic 5 Analytical & Descriptive Questions

Home
Ask Doubt
Profile