Find the intervals of the values of $a$ for which the line $y + x = 0$ bisects two chords drawn from the point $(\frac{1 + \sqrt{2} a}{2}, \frac{1 - \sqrt{2} a}{2})$ to the circle $2 x^{2} + 2 y^{2} - (1 + \sqrt{2} a) x - (1 - \sqrt{2} a) = 0$

Video Solution

Text Solution

Verified by Experts

Given, $2 x^{2} + 2 y^{2} - (1 + \sqrt{23} a) x - (1 - \sqrt{2} a) y = 0$
$\Rightarrow x^{2} + y^{2} - (\frac{1 + \sqrt{2} a}{2}) x - (\frac{1 - \sqrt{2} a}{2}) y = 0$
Since, y + x = 0 bisects two chords of this circle, mid points of the chords must be of the form $(α, - α)$ .

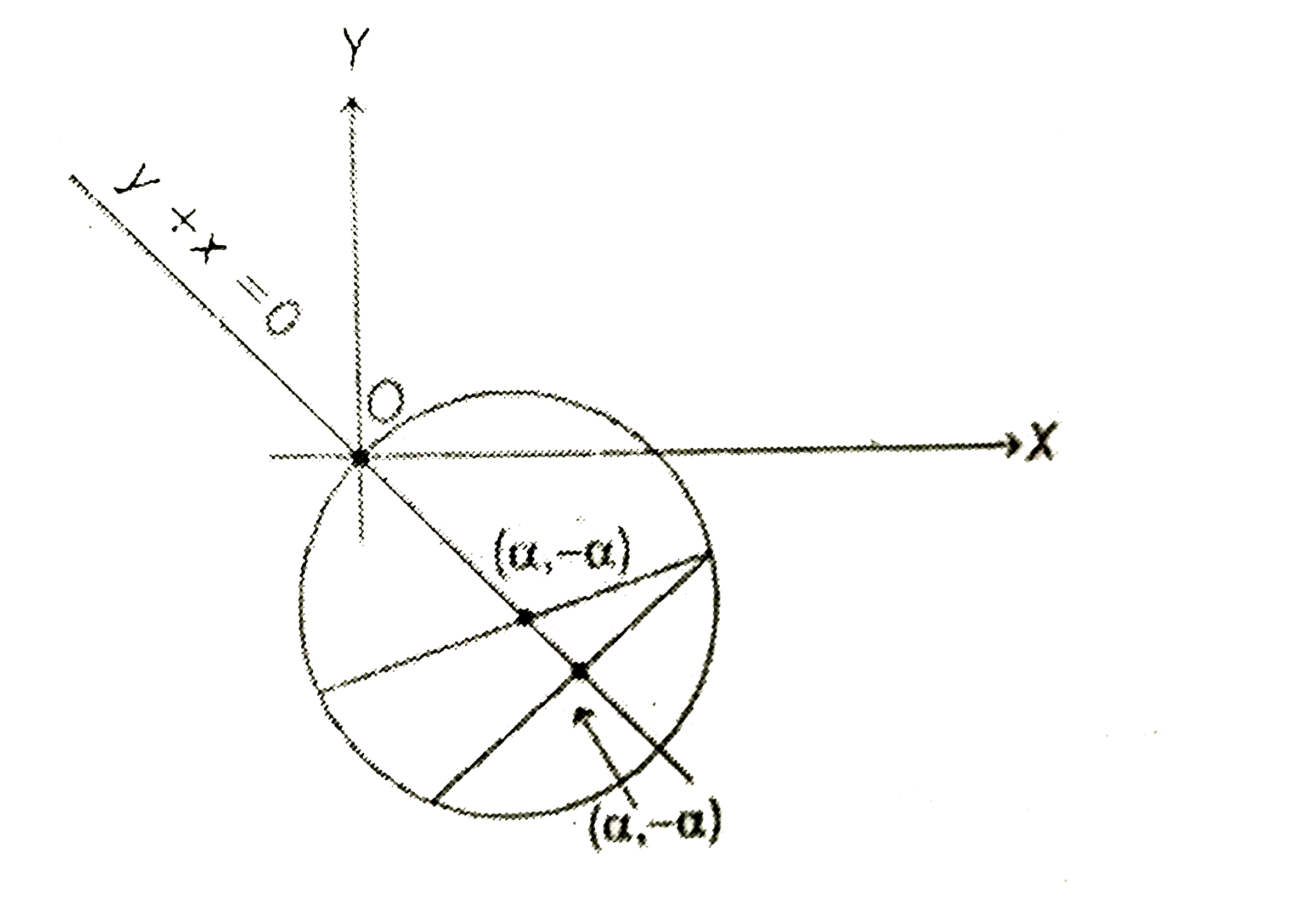
Equation of the chord having $(α, - α)$ as mid point is
$T = S_{1}$
$\Rightarrow x α + y (- α) - (\frac{1 + \sqrt{2} a}{4}) (x + α) - (\frac{1 - \sqrt{2} a}{4}) (y - α)$
$a^{2} + {(- α)}^{2} - (\frac{1 + \sqrt{2} a}{2}) α - (\frac{1 - \sqrt{2} a}{2}) (- α)$
$\Rightarrow 4 x α - 4 y α - (1 + \sqrt{2} α) x - (1 + \sqrt{2} a) α$
$- (1 - \sqrt{2} a) y + (1 - \sqrt{2} a) α$
$4 α^{2} + 4 α^{2} - (1 + \sqrt{2} a) \cdot 2 α + (1 - \sqrt{2} a) \cdot 2 α$
$\Rightarrow 4 a x - 45 a y - (1 + \sqrt{2} a) x - (1 - \sqrt{2} a) y$
$= 8 α^{2} - (1 + \sqrt{2} a) α + (1 - \sqrt{2} a) α$
But this chord will pass through the point $(\frac{1 + \sqrt{2} a}{2}) f - 4 α (\frac{1 - \sqrt{2} a}{2}) - \frac{(1 + \sqrt{2} a) (1 + \sqrt{2} a)}{2}$
$- \frac{(1 - \sqrt{2} a) (1 - \sqrt{2} a)}{2}$
$= 8 α^{2} - 2 \sqrt{2} a α$
$\Rightarrow 2 α [(1 + \sqrt{2} a - 1 + \sqrt{2} a)] = 8 α^{2} - 2 \sqrt{2} a α$
$\Rightarrow 4 \sqrt{2} α - \frac{1}{2} {[2 + 2 \sqrt{2} a)}^{2}] = 8 α^{2} - 2 \sqrt{2} a α$
$[∴ {(a + b)}^{2} + {(a - b)}^{2} = 2 a^{2} + 2 b^{2}]$
$\Rightarrow 8 α^{2} - 6 \sqrt{2} α + 1 + 2 a^{2} = 0$
But this quadratic equation will have two distinct roots, if
${(6 \sqrt{2} a)}^{2} - 4 (8) (1 + 2 a^{2}) > 0$
$\Rightarrow 72 a^{2} - 32 (1 + 2 a^{2}) > 0$
$\Rightarrow 8 a^{2} - 32 > 0$
$\Rightarrow a^{2} - 4 > 0$
$\Rightarrow a < - 2 \cup a > 2$
Therefore, $a \in (- \infty, - 2) \cup (2, \infty)$ .

Updated on:21/07/2023

If $x \cdot y = \sqrt{x^{2} + y^{2}}$ the value of $(1 \cdot 2 \sqrt{2}) (1 \cdot - 2 \sqrt{2})$ is
A(-7)
B0
C2
D9
If two distinct chords drawn from the point $(2 \sqrt{2} sin θ, \frac{1}{\sqrt{2}})$ to the circle.
$x^{2} + y^{2} = 2 \sqrt{2} sin θ x + \frac{1}{\sqrt{2}} y$ ( $θ$ is a parameter) are bisected by x -axis, then the exhaustive set in which $θ$ lies is
A $(n π + \frac{π}{4}, n π + \frac{3 π}{4}), n \in I$
B $(n π + \frac{π}{6}, n π + \frac{5 π}{6}), n \in I$
C $(2 n π + \frac{π}{4}, 2 n π + \frac{3 π}{4}), n \in I$
D $(2 n π, (2 n + 1) π), n \in I$
If $2 x = \sqrt{a} - \frac{1}{\sqrt{a}}$ , then the value of $\frac{\sqrt{x^{2} + 1}}{x + \sqrt{x^{2} + 1}}$ is
Aa+1
B $\frac{1}{2} (\frac{a + 1}{a})$
C $\frac{1}{2} (\frac{a - 1}{a})$
D $a - 1$