The circle C1 : x2 + y2 = 3, with centre at O, intersects the parabola x2 = 2y at the point P in the first quadrant. Let the tangent to the circle C1 at P touches other two circles C2 and C3 at R2 and R3, respectively. Suppose C2 and C3 have equal radii 2 3 and centres Q2 and Q3, respectively.

A

$Q_{2} Q_{3} = 12$

B

$R_{2} R_{3} = 4 \sqrt{6}$

C

area of the $Δ P R_{2} R_{3} is 6 \sqrt{2}$

D

area of the $Δ P Q_{2} Q_{3} is 4 \sqrt{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

Given $C_{1} : x^{2} + y^{2} = 3$ intersects the parabola $x^{2} = 2 y$ .

On solving $x^{2} + y^{2} = 3 and x^{2} = 2 y$ , we get
$y^{2} + 2 y = 3$
$\Rightarrow y^{2} + 2 y - 3 = 0$
$\Rightarrow (y + 3) (y - 1) = 0$
$∴ y = 1, - 3 [neglecting y = - 3, a s - \sqrt{3} \leq y \leq \sqrt{3}]$
$∴ y = 1 \Rightarrow x = \pm \sqrt{2}$
$\Rightarrow P (\sqrt{2}, 1) \in I quadrant$
Equation of tangent at $P \sqrt{2}, 1) to C_{1} : x^{2} + y^{2} = 3$ is
$\sqrt{2} x + 1 \cdot y = 3 ... (i)$
Now, let the centres of $C_{2} and C_{3}$ at $R_{2} and R_{3}$ shown as below

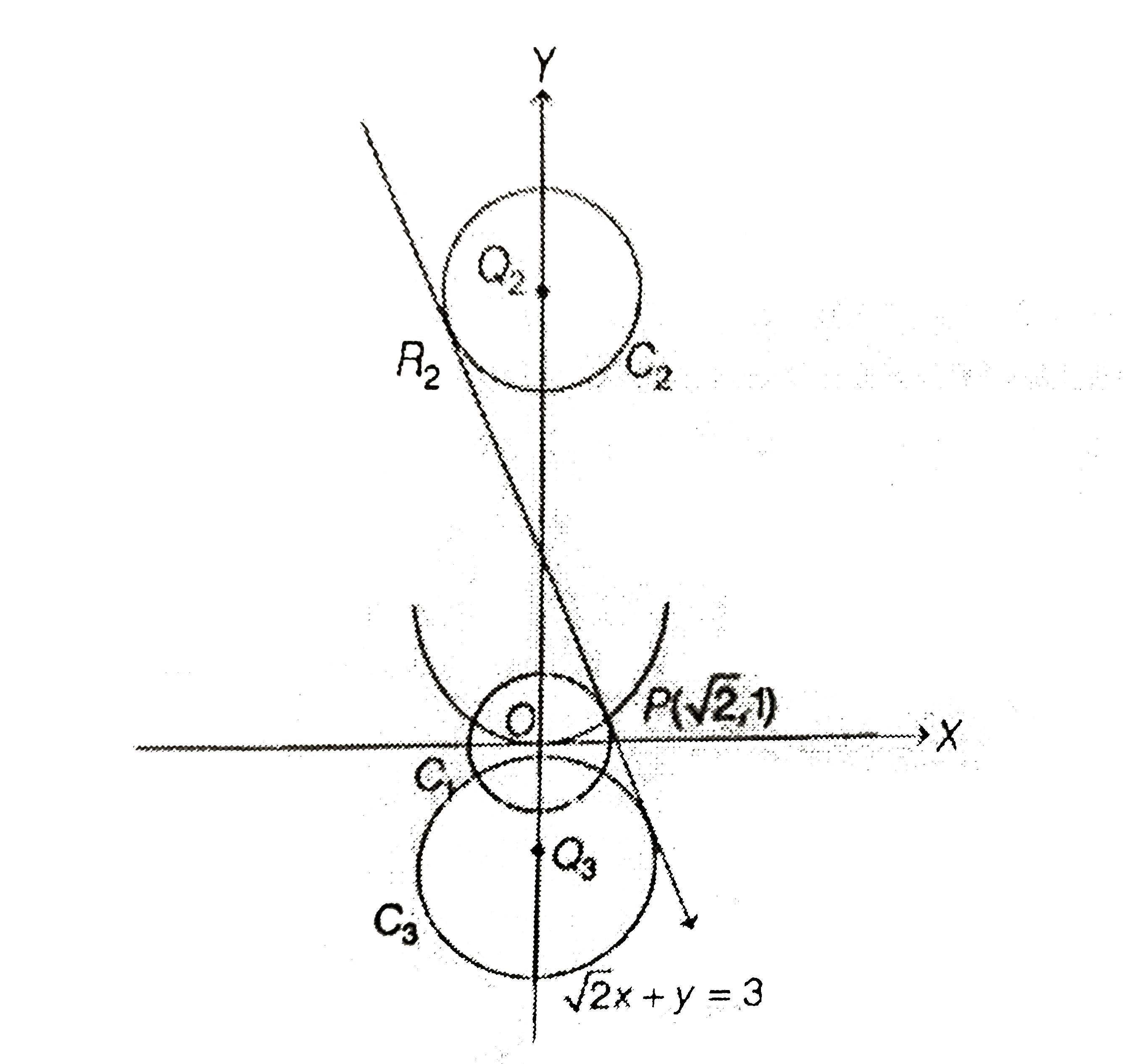
Let $Q_{2}$ be (0,k) and radius is $2 \sqrt{3}$ .
$∴ \frac{| 0 + k - 3 |}{\sqrt{2 + 1}} = 2 \sqrt{3}$
$\Rightarrow | k - 3 | = 6$
$\Rightarrow h = 9, - 3$
$∴ Q_{2} (0, 9) and Q_{3} (0, - 3)$
Hence, $Q_{2} Q_{3} = 12$
$∴$ option (a) is correct.
Also, $R_{2} R_{3}$ is common internal tangent to $C_{2} and C_{3}$ ,
and $r_{2} = r_{3} = 2 \sqrt{3}$
$R_{2} R_{3} = \sqrt{d^{2} - {(r_{1} + r_{2})}_{1}^{2}} = \sqrt{12^{2} - {(4 \sqrt{3})}^{2}}$
$= \sqrt{144 - 48} = \sqrt{96} = 4 \sqrt{6}$

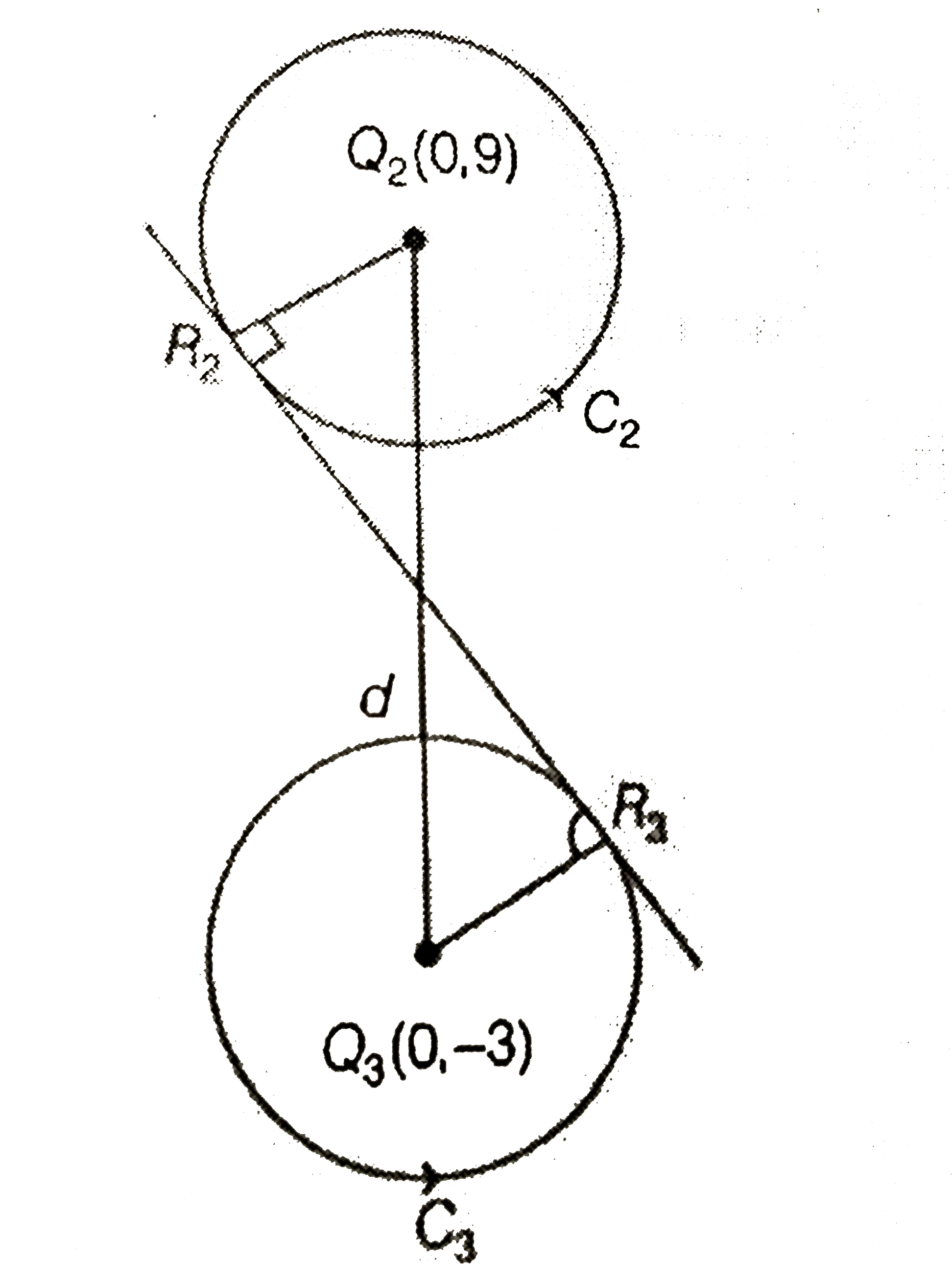
$∴$ (b) is correct.
$∴$ Length of perpendicular from $O (0, 0) to R_{2} R_{3}$ is equal to radius of $C_{1} = \sqrt{3}$
$∴ Area of Δ P Q_{2} Q_{3} = \frac{1}{2} Q_{2} Q_{3} \times \sqrt{2} = \frac{\sqrt{2}}{2} \times 12 = 6 \sqrt{2}$
$∴$ Option (c) is correct.
Also, area of $Δ P Q_{2} Q_{3} = \frac{1}{2} Q_{2} Q_{3} \times \sqrt{2} = \frac{\sqrt{2}}{2} \times 12 = 6 \sqrt{2}$
$∴$ Option (d) is incorrect.

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The circle $C_{1} : x^{2} + y^{2} = 3$ , with cenre at O, intersects the parabola $x^{2} = 2 y$ at the point P in the first quadrant. Let the tangent to the circle $C_{1}$ at P touches other two circles $C_{2}$ and $C_{3}$ at $R_{2}$ and $R_{3}$ respectively. Suppose $C_{2}$ and $C_{3}$ have equal radii $2 \sqrt{3}$ and centres $Q_{2}$ and $Q_{3}$ respectively. If $Q_{2}$ and $Q_{3}$ lie on the y-axis, then $Q_{2} Q_{3} =$
A3
B6
C9
D12
Question 2 - Select One or More
The circle $C_{1} : x^{2} + y^{2} = 3$ , with centre at O, intersects the parabola $x^{2} = 2 y$ at the point P in the quadrant. Let the tangent to the circle $C_{1}$ at P touches other tqo circles $C_{2} and C_{3}$ at $R_{2} and R_{3}$ , respectively. Suppose $C_{2} and C_{3}$ have equal radii $2 \sqrt{3}$ and centres $Q_{2} and Q_{3}$ . respectively. If $Q_{2} and Q_{3}$ lie on the y-axis, then
A $Q_{2} Q_{3} = 12$
B $R_{2} R_{3} = 4 \sqrt{6}$
Carea of the triangle $O R_{2} R_{3} is 6 \sqrt{2}$
Darea of the triangle $P Q_{2} Q_{3} is 4 \sqrt{2}$
Question 3 - Select One
A circle $C_{1}$ is drawn having any point P on x-axis as its centre and passing through the centre of the circle (C ) $x^{2} + y^{2} = 1$ . A common tangent to $C_{1}$ to C intersects the circle at Q and R respectively. Then Q(x,y) always satisfies
A $x^{2} - 1 = 0$
B $x^{2} + y^{2} = 1$
C $y^{2} - 1 = 0$
Dnone of these

IIT JEE PREVIOUS YEAR-CIRCLE-Topic 3 Objective Question II

Home
Ask Doubt
Profile