Let RS be the diameter of the circle $x^{2} + y^{2} = 1,$ where S is the point $(1, 0)$ Let P be a variable apoint (other than $R and S$ ) on the circle and tangents to the circle at $S and P$ meet at the point Q.The normal to the circle at P intersects a line drawn through Q parallel to RS at point E. then the locus of E passes through the point(s)- (A) $(\frac{1}{3}, \frac{1}{\sqrt{3}})$ (B) $(\frac{1}{4}, \frac{1}{2})$ (C) $(\frac{1}{3}, - \frac{1}{\sqrt{3}})$ (D) $(\frac{1}{4}, - \frac{1}{2})$

A

$(\frac{1}{3}, \frac{1}{\sqrt{3}})$

B

$(\frac{1}{4}, \frac{1}{2})$

C

$(\frac{1}{3}, - \frac{1}{\sqrt{3}})$

D

$(\frac{1}{4}, - \frac{1}{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C

Given, RS is the diameter of $x^{2} + y^{2} = 1$ .
Here, equation of the tangent at $P (cos θ, sin θ) is x cos θ + y sin θ = 1$ .

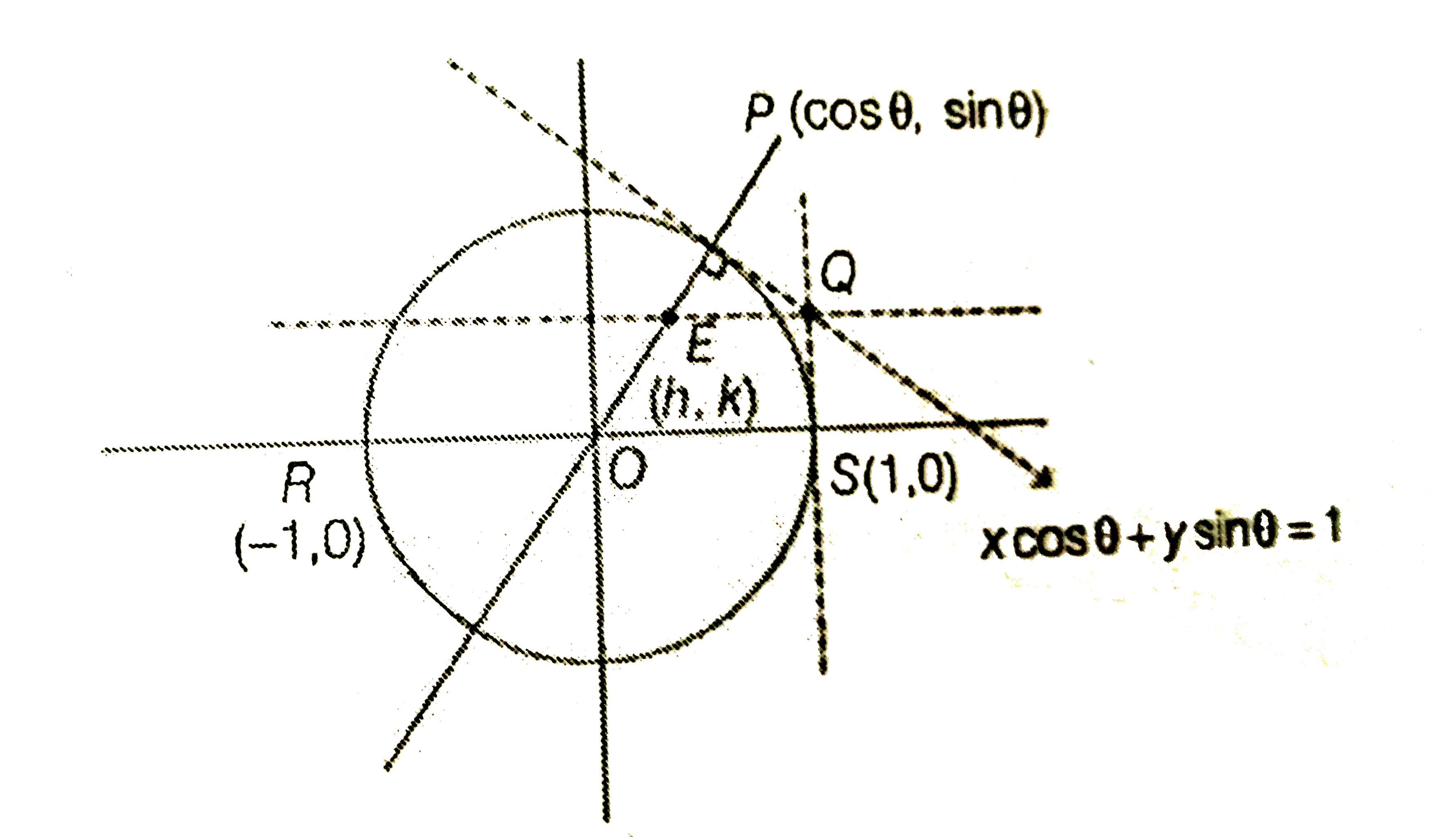
Intersecting with x = 1,
$y = \frac{1 - cos θ}{sin θ}$
$∴ Q (1 \frac{1 - cos θ}{sin θ})$
$∴$ Equation of the line through Q parallel to RS is
$y = \frac{1 - cos θ}{sin θ} = \frac{2 {sin}^{2} \frac{θ}{2}}{2 sin \frac{θ}{2} cos \frac{θ}{2}} = tan \frac{θ}{2} ... (i)$
Normal at $P : y = \frac{sin θ}{cos θ} \cdot x$
$\Rightarrow y = x tan θ ... (i i)$
Let their point of intersection be (h, k).
Then, $h = tan \frac{θ}{2} and k = h tan θ$
$∴ k = h ⎛ ⎝ \frac{2 tan \frac{θ}{2}}{1 - {tan}^{2} \frac{θ}{2}} ⎞ ⎠ \Rightarrow k = \frac{2 h - k}{1 - k^{2}}$
$\Rightarrow k (1 - k^{2}) = 2 h k$
$∴ Locus for point E : 2 x = (1 - y^{2}) ... (i i i)$
When $x = \frac{1}{3}$ , then
$1 - y^{2} = \frac{2}{3} \Rightarrow y^{2} = 1 - \frac{2}{3} \Rightarrow y = \pm \frac{1}{\sqrt{3}}$
$∴ (\frac{1}{3}, \pm \frac{1}{\sqrt{3}}) satisfy 2 x = 1 - y^{2}$ .
when $x = \frac{1}{4}$ , then
$1 - y^{2} = \frac{2}{4} \Rightarrow y^{2} = 1 - \frac{1}{2} \Rightarrow y = \pm \frac{1}{\sqrt{2}}$
$∴ (\frac{1}{4}, \pm \frac{1}{2}) does not satisfy 1 - y^{2} = 2 x$ .

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A tangent to the circle $x^{2} + y^{2} = 1$ through the point (0, 5) cuts the circle $x^{2} + y^{2} = 4$ at P and Q. If the tangents to the circle $x^{2} + y^{2} = 4$ at P and Q meet at R, then the coordinates of R are
A $(8 \sqrt{6} / 5, 4 / 5)$
B $(8 \sqrt{6} / 5), - 4 / 5)$
C $(- 8 \sqrt{6} / 5), - 4 / 5)$
Dnone of these
Question 2 - Select One
Tangents to a circle at points P and Q on the circle intersect at a point R. If PQ= 6 and PR= 5 then the radius of the circle is
A $\frac{13}{3}$
B4
C $\frac{15}{4}$
D $\frac{16}{5}$
Question 3 - Select One
Let P and Q be two points on a circle with centre O. If two tan gents of the circle through P and O meet at A with $∠ P A Q = 48^{\circ}$ , then $∠ A P Q$ is
A $96^{\circ}$
B $48^{\circ}$
C $66^{\circ}$
D $60^{\circ}$

IIT JEE PREVIOUS YEAR-CIRCLE-Topic 3 Objective Question II

Home
Ask Doubt
Profile