Three circles touch each other externally. The tangents at their point of contact meet at a point whose distance from a point of contact is 4. Then, the ratio of their product of radii to the sum of the radii is
The correct Answer is:16:1
Suppose the circle have centres at C1,C2andC3 with Radius R1,R2andR3 respectively.Let the circle touch at A,B and C. Let the common tangents at A,B and C meet at O. We have OA = Ob = OC = 4 [given] Now, the circle with centre at O and passing through A, B and C is the incircle of the triangle C1C2C3 (becauseOA⊥C1C2).
Therefore, the inradius of ΔC1C2C3 is 4 .
and r=Δs ...(i)
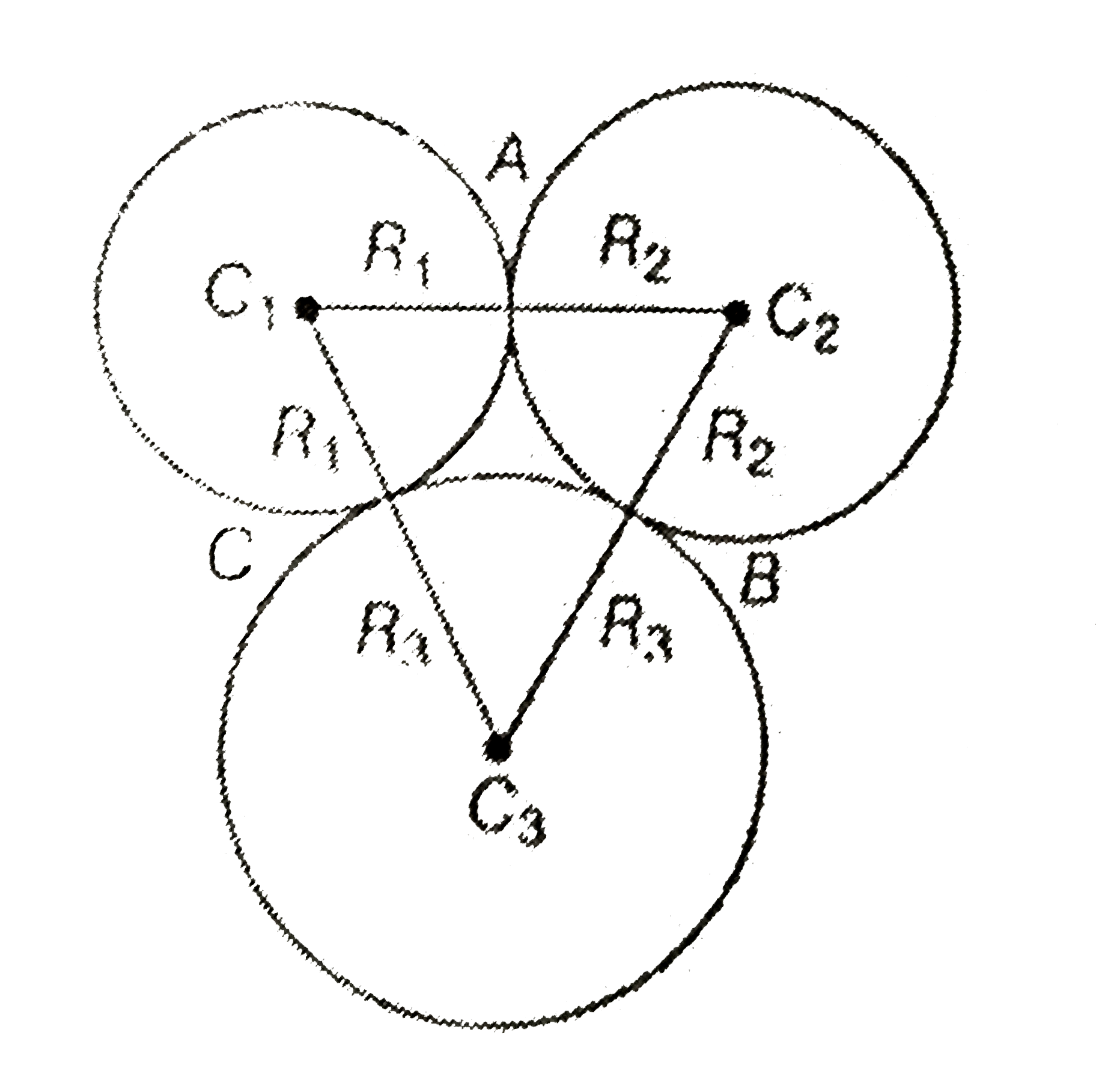
Nowm perimeter of a triangle
2s=R1+R2+R2+R3+R3+R1
⇒2s=2(R1+R2+R3)
⇒s=R1+R2+R3
and Δ=√s(s−a)(s−b)(s−c)
=√(R1+R2+R3)(R3)(R2)(R1)
From Eq. (i), 4=√(R1R2R3)(R1+R2+R3)R1+R2+R3
⇒16=√R1R2R3(R1+R2+R3)R1+R2+R3
⇒16=R1R2R3R1+R2+R3
Topper's Solved these Questions
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 3 Equation of Tangent, Normal and Length of Tangents
Explore 9 Videos
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 3 Objective Question II
Explore 2 Videos
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 2 Match the Columns
Explore 1 Video
- BINOMIAL THEOREMBook:IIT JEE PREVIOUS YEARChapter:BINOMIAL THEOREMExercise:Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
Explore 8 Videos
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)
Explore 1 Video
Similar Questions
Three circle touches one another externally. The radius of circles are three consecutive integers. The tangent at their point of contact meet at a point whose distance from a point of contact is 4. The ratio of radius of largest to smallest circle is
View SolutionThree circles with radius r1,r2,r3 touch one another externally. The tangents at their point of contact meet at a point whose distance from a point of contact is 2. The value of (r1r2r3r1+r2+r3) is equal to
View Solution
Knowledge Check
Three circles touch one-another externally. The tangents at their point of contact meet at a point whose distance from a point contact is 4. Then, the ratio of the product of the radii of the sum of the radii of circles is
A16:1B1:16C8:1DNone of theseThree circles touch each other externally. The distance between their centre is 3 cm, 4 cm and 5 cm. Find the radii of the circles :
A1 cm, 2 cm, 3 cmB12cm,32cm,52cmC1 cm, 2.5 cm, 3.5 cmDNone of theseThree circles touch each other externally. The distance between their centre is 3 cm, 4 cm and 5 cm. Find the radii of the circles :
A3cm, 2cm, 4cmB3cm, 4cm, 1cmC1 cm, 2.5 cm, 3.5 cmD1 cm, 2 cm, 4 cm
Three circles touch one-anothet externally and tangent at their point of contact meet at a point. If their radii be r1,r2,r3 then the distance of this point from eithet ot their points of contact is ……
View SolutionThree circles whose radii are a,b and c and c touch one other externally and the tangents at their points of contact meet in a point. Prove that the distance of this point from either of their points of contact is (abca+b+c)12.
View SolutionThree circles are such that each touch the other two externally. The common tangents are concurrent at 'p'. The length of the tangent to each circle is P. The ratio of the product of their radii to sum of their radii is
View SolutionIf two circles touch each other (internally or externally); the point of contact lies on the line through the centres.
View SolutionThree circles touch each other externally. The distance between their centre is 5 cm, 6 cm and 7 cm. Find the radii of the circles :
View Solution

