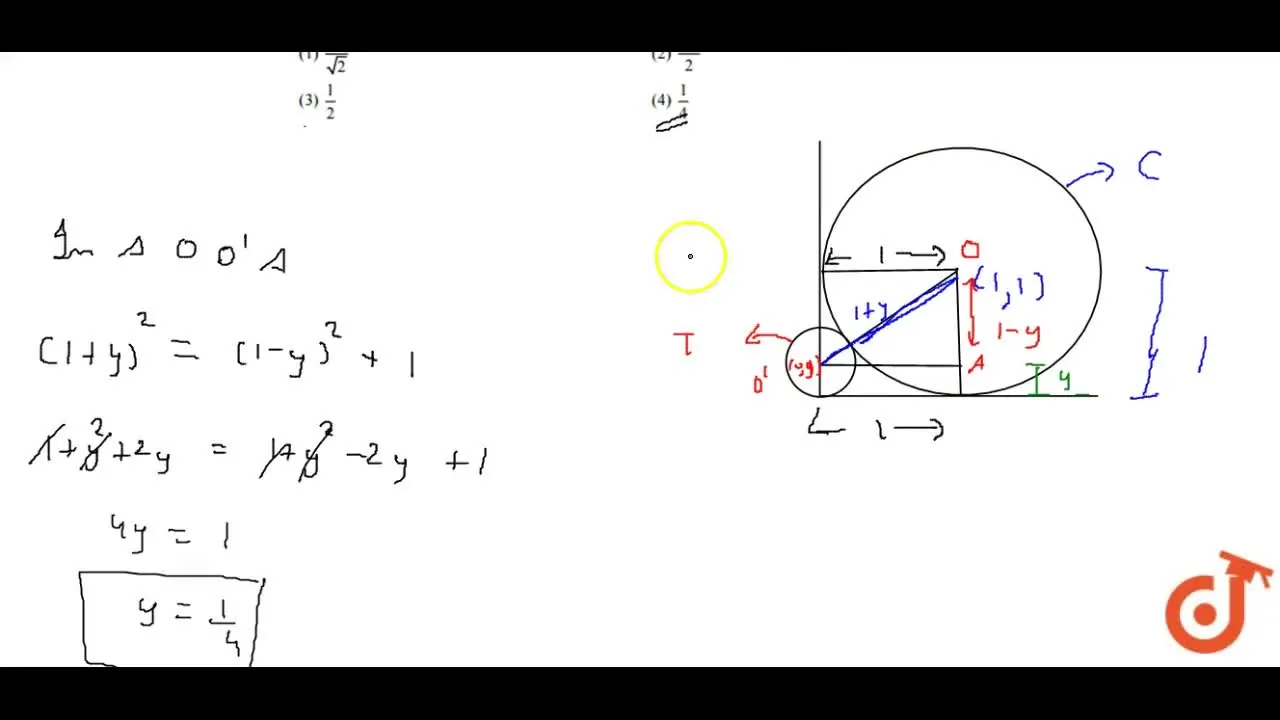
Let C be the circle with centre at (1, 1) and radius = 1. If T is the circle centred at (0, y), passing through origin and touching the circle C externally, then the radius of T is equal to (1) √3√2 (2) √32 (3) 12 (3) 14
√3√2
√32
12
14
The correct Answer is:D
Plan Use the property, when two circles touch each other externally, then distance between the centre I s equal to sum of their radii, to get required radius.
Let the coordinate of the centre of T be (0, k).
Distance between their centre
k+1=√1+(k−1)2 [∴C1C2=k+1]
⇒K+1=√1+k2+1−2k
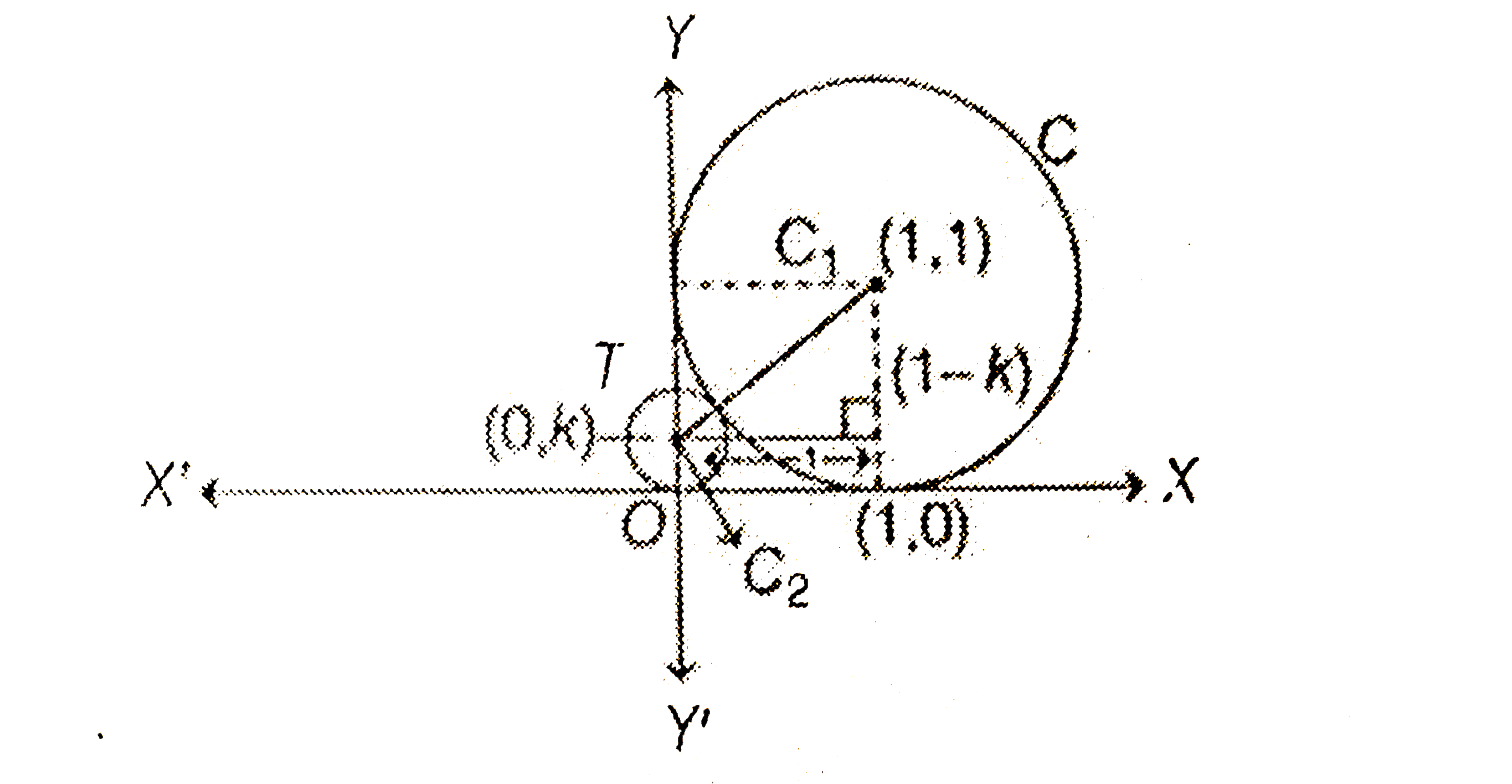
⇒k+1=√k2+2−2k
⇒k2+1+2k=k2+2−2k
⇒k=14
So, the radius of circle T is K, i. e.14.
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 2 Objective Question II2videos
CIRCLE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 2 Passage Based Problems3videos
CIRCLE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 1 Paragraph Based Questions2videos
CIRCLE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - BINOMIAL THEOREMEXERCISE - Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )8videos
BINOMIAL THEOREM
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)1videos
COMPLEX NUMBERS
Similar Questions
Let C be the circle with centre at (1, 1) and radius 1 If Tis the circle centred at (0, y), passing through origin and touching the circle C externally, then the radius of T is equal to V3 (a) 4
View SolutionLet C be the circle with centre (1,1) and radius 1 . If T is the circle centred at (0,y) , passing through origin and touching the circle C externally , then the radius of T is equal to
View SolutionLet C be the circle with centre at (1, 1) and radius = 1. If T is the circle centred at (0, y), passing through origin and touching the circle C externally, then the radius of T is equal to (1) √3√2 (2) √32 (3) 12 (3) 14
View SolutionLet C be the circle with centre (1,1) and radius 1.If T is the circle centered at (0,k) passing through origin and touching the circle C externally then the radius of T is equal to (a) √3√2 (b) √32 (c) 12 (d) 14
View Solution1) 1/5 2) 10 3) 10v2 4) 5v2 Let C be the circle with centre at (1,1) and radius -1. If T is the circle centered at (0,y), passing through origin and touching the circle C externally, then the radius of T is equal to 56. 3 2 1) 2) 3) 4)
View SolutionFind the equation of the circle with centre(-1,-3) and radius √3
View SolutionFind the equation of the circle with : Centre(1,1)andradius√2.
View SolutionIf the radisu of the circle passing through the origin and touching the line x+y=2 at (1,1) is r units, then the value of 3√2r is
View SolutionEquation of circle centred at (2,-3) , and passing through (-1,2) , is
View SolutionEquation of circle centred at (1,-1) , and passing through (3,2) , is
View Solution