Let x2+y2−2x−2y−2=0 and x2+y2−6x−6y+14=0 are two circles C1,C2 are the centre of circles and circles intersect at P,Q find the area of quadrilateral C1PC2Q
8
4
6
9
The correct Answer is:B
Given circles,
x2+y2−2x−2y−2=0 ...(i)
and x2+y2−6x−6y+14=0 ...(ii)
are intersecting each other orthogonally, because
2(1)(3)+2(1)(3)=14-2
[∴ two circle are intersected orthogonally if 2g1g2+2f1f2=c1+c2]
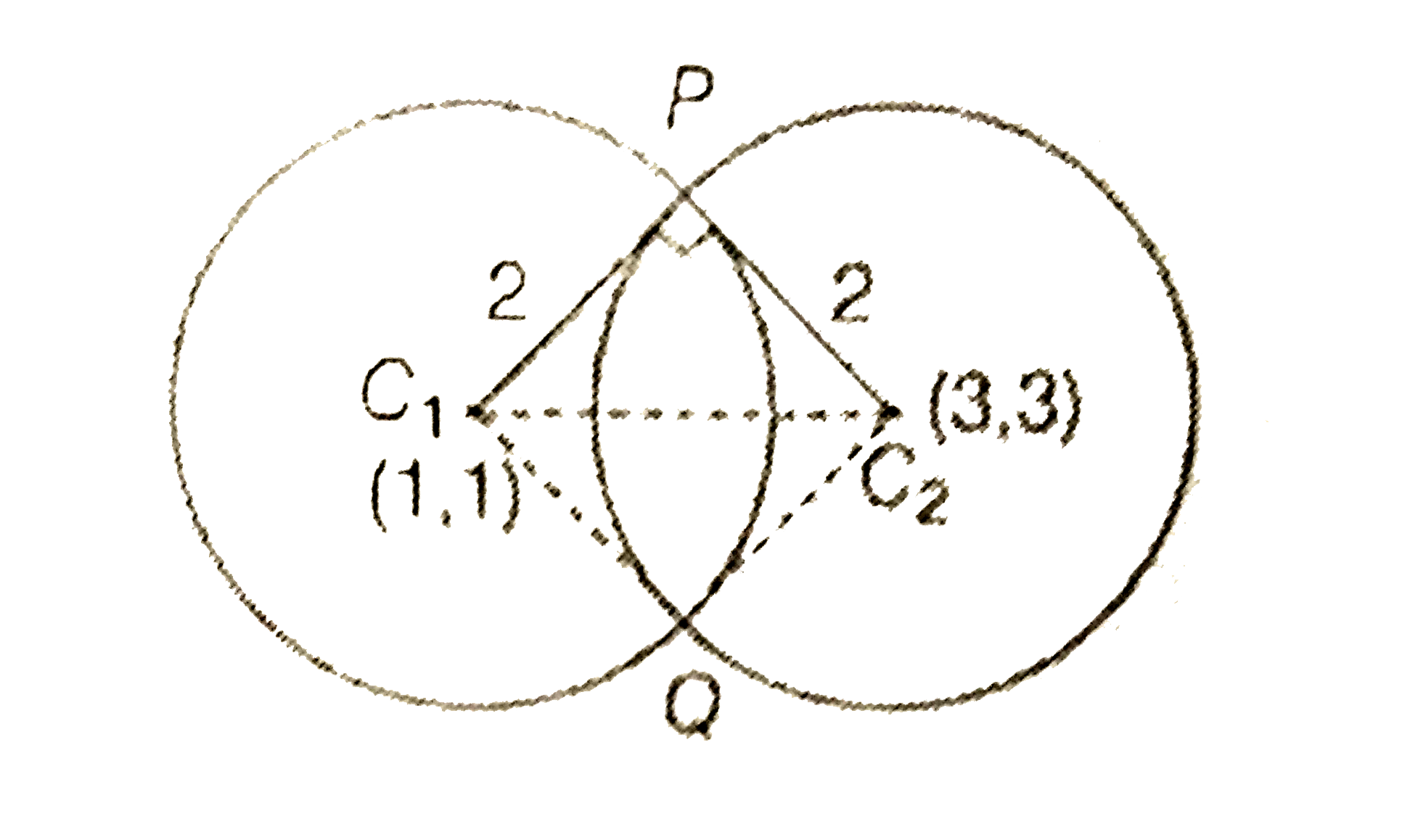
So, area of quadrilateral
PC1QC2=2×ar(ΔPC1C2).
=2×(12×2×2)=4 sq units.
Topper's Solved these Questions
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 2 Objective Question II
Explore 2 Videos
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 2 Passage Based Problems
Explore 3 Videos
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 1 Paragraph Based Questions
Explore 2 Videos
- BINOMIAL THEOREMBook:IIT JEE PREVIOUS YEARChapter:BINOMIAL THEOREMExercise:Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
Explore 8 Videos
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)
Explore 1 Video
Similar Questions
Let C1 and C2 be the centres of the circles x2+y2−2x−2y−2=O and x2+y2−6x−6y+14=0 respectively.If P and Q are the points of intersection of these circles,then the area (in sq.units) of the quadrilateral PC1QC2 is
View SolutionIf x2+y2−4x+6y+c=0represents a circle with radius 6 then c is
View Solution
Knowledge Check
x2+y2+6x=0 and x2+y2–2x=0 are two circles, then
AThey touch each other externallyBThey touch each other internallyCArea of triangle formed by their common tangents is 3√3 sq. units.DTheir common tangents do not form any triangleLet C1andC2 be the centres of the circles x2+y2−2x−2y−2=0andx2+y2−6x+14=0 respectively. If P and Q are the points of intersection of these circles, then the area (in sq. units) of the quadrilateral PC1QC2 is:
A8B6C9D4Let C1andC2 be the circles x2+y2−2x−2y−2=0 and x2+y2−6x−6y+14=0 respectively. If P and Q are points of intersection of these circles, then the area (in sq. units ) of the quadrilateral PC1QC2 is :
A4B9C6D8
For the four circles M, N, O and P, following four equations are given :
Circle M : x2+y2=1
Circle N : x2+y2–2x=0
Circle 0 : x2+y2−2x−2y+1=0
Circle P : x2+y2–2y=0
If the centre of circle M is joined with centre of the circle N, further centre of circle N is joined with centre of the circle O, centre of circle O is joined with the centre of circle P and lastly, centre of circle P is joined with centre of circle M, then these lines form the sides of a :
View SolutionA diameter of x2+y2−2x−6y+6=0 is a chord to circle centre (2, 1), then radius of the circle is
View SolutionLet A be the centre of the circle x2+y2−2x−4y−20=0 .If the tangents at the points B(1,7)andD(4,-2) on the circle meet at C , then find the area of the quadrilateral ABCD .
View SolutionFrom the point P(16,7), tangents PQ and PR are drawn to the circle x2+y2−2x−4y−20=0. If C is the centre of the circle, then area of quadrilateral PQCR is
View SolutionFrom the point P(16, 7) tangents PQ and PR are drawn to the circle x2+y2−2x−4y−20=0. If c be the centre of the circle, then area of quadrilateral PQCR is
View Solution

