A particle starts from a point $z_{0} = 1 + i$ where $i = \sqrt{- 1}$ . lt moves horizontally away from origin by 2 units and then vertically away from origin by 3 units to reach a point $z_{1}$ , From $z_{1}$ particle moves $\sqrt{5}$ units in the direction of $2 ˆ i + 3 ˆ j$ and then it moves through Ã n angle of $cos e c^{- 1} 2$ in anticlockwise direction of a circle with centre at origin to reach a point $z_{2}$ . The arg $z_{1}$ is given by

A

$6 + 7 i$

B

$- 7 + 6 i$

C

$7 + 6 i$

D

$- 6 + 7 i$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

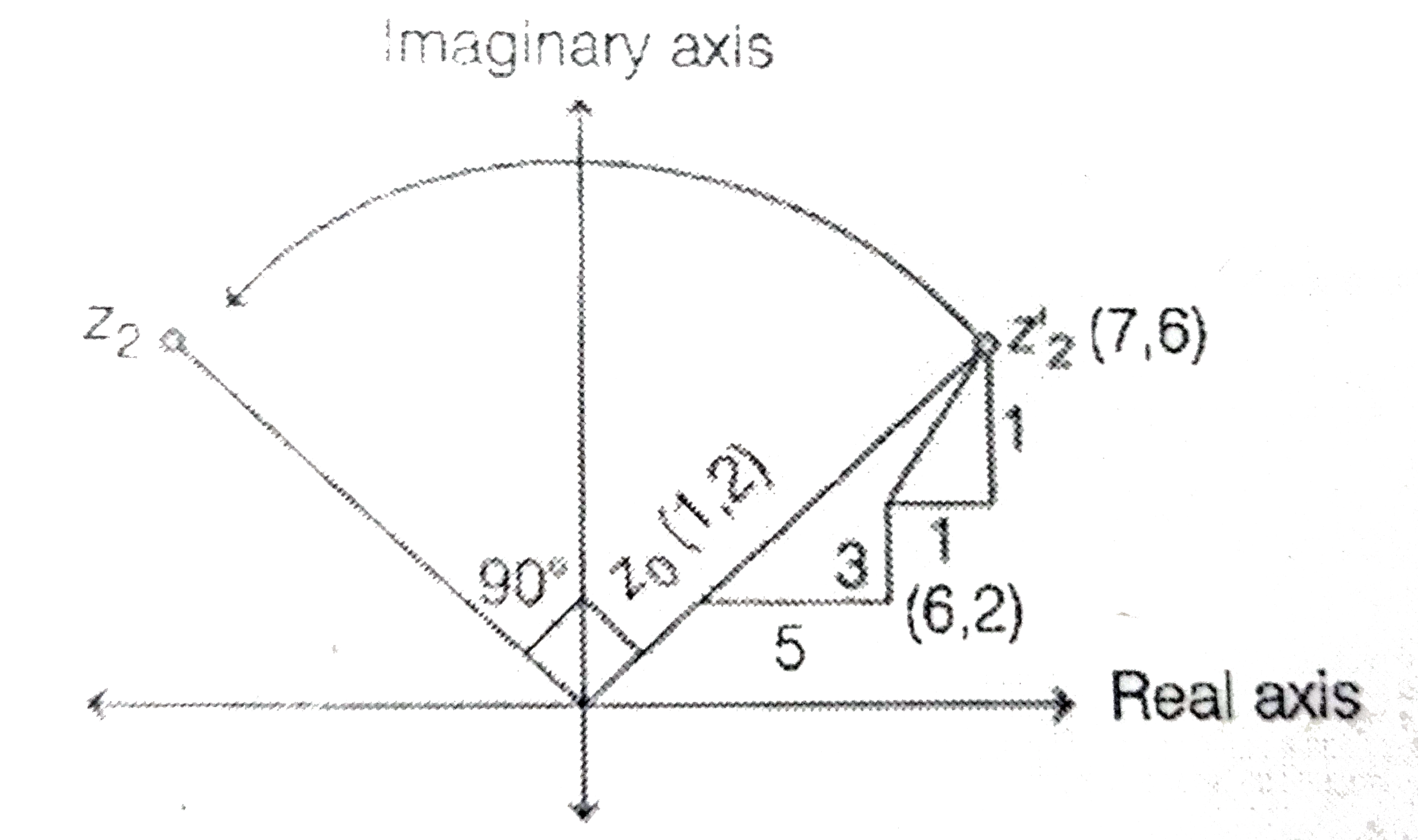
$z_{2} = (6 + \sqrt{2} {cos 45}^{\circ}, 5 + \sqrt{2} {sin 45}^{\circ})$ = (7,6)= 7 + 6i By rotaion about (0,0)
$\frac{z_{2}}{z_{2}} = e^{I π / 2} \Rightarrow z_{2} = z_{2} (e^{i \frac{π}{2}})$
$= (7 + 6 i) (cos \frac{π}{2} + i sin \frac{π}{2}) = (7 + 6 i) (i) = - 6 + 7 i$

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle $P$ starts from the point $z_{0} = 1 + 2 i,$ where $i = \sqrt{- 1}$ . It moves first horizontally away from origin by 5 units and then vertically away from origin by 3 units to reach a point $z_{1} .$ From $z_{1}$ the particle moves $\sqrt{2}$ units in the direction of the vector $ˆ i + ˆ j$ and then it moves through an angle $\frac{π}{2}$ in anticlockwise direction on a circle with centre at origin, to reach a point $z_{2} .$ The point $z_{2}$ is given by $6 + 7 i$ (b) $- 7 + 6 i$ $7 + 6 i$ (d) $- 6 + 7 i$
A6 + 7i
B $- 7 + 6 i$
C7 +6i
D $- 6 + 7 i$
Question 2 - Select One
A particle P starts from the point $z_{0} = 1 + 2 i$ , where $i = \sqrt{- 1}$ . It moves first horizontally away from origin by 5 units and then vertically away from origin by 3 units in the direction of the vector $ˆ i + ˆ j$ and then it moves through an angle $\frac{π}{2}$ in anticlockwise direction on a circle with center at origin, to reach a point $z_{2}$ . The point $z_{2}$ is given by
A $6 + 7 i$
B $- 7 + 6 i$
C $7 + 6 i$
D $- 6 + 7 i$
Question 3 - Select One
$z_{1}, z_{2}, z_{3}$ are the vertices of an equilateral triangle taken in counter clockwise direction. If its circumference is at the origin and $z_{1} = 1 + i$ , then
A $z_{2} = z_{1} e^{i 2 π / 3}, z_{3} = e^{π / 3}$
B $z_{2} = z_{1} e^{i 2 π / 3}, z_{3} = z_{1} e^{i 4 π / 3}$
C $z_{2} = z_{1} e^{i 4 π / 3}, z_{3} = z_{1} e^{i 2 π / 3}$
D $z_{2} = z_{1} e^{i π / 3}, z_{3} = z_{1} e^{i 2 π / 3}$

IIT JEE PREVIOUS YEAR-COMPLEX NUMBERS-TOPIC 4 ROTATION OF A COMPLEX NUMBER (OBJECTIVE QUESTION I)(ONLY ONE CORRECT OPTION)

Home
Ask Doubt
Profile