Let $z_{1} = 10 + 6 i$ and $z_{2} = 4 + 6 t$ If $z$ is any complex number such that the argument of $\frac{(z - z_{1})}{(z - z_{2})}$ is $\frac{π}{4},$ then prove that $| z - 7 - 9 i | = 3 \sqrt{2}$ .

Video Solution

Text Solution

Verified by Experts

Since $z_{1} = 10 + 6 i, z_{2} = 4 + 6 i$
and arg $(\frac{z - z_{1}}{z - z_{2}}) - (\frac{π}{4})$ represente lecue of z is a circle shown as form the figure whose center is (7,y) and $∠ A O B = 90^{\circ}$ clearly OC = 9 $\Rightarrow$ OD = 6 + 3 =9
$∴$ Center = (7,9) and readius $= \frac{6}{\sqrt{2}} = 3 \sqrt{2}$

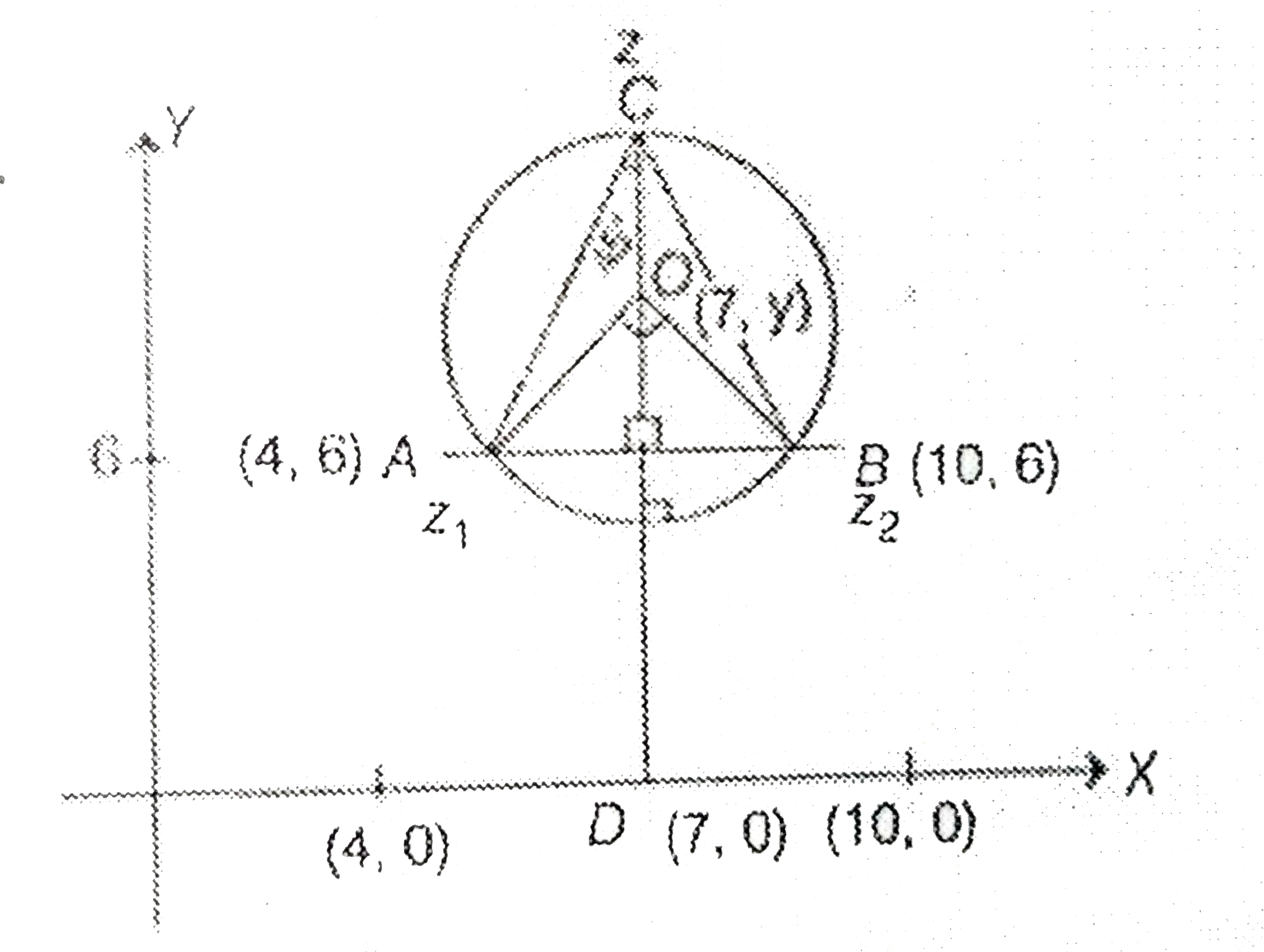
$\Rightarrow$ Equation of circle is $| z - (7 + 9 i) | = 3 \sqrt{2}$

Updated on:21/07/2023

|

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let $Z_{1}$ and $Z_{2}$ be any two non-zero complex number such that $3 | z_{1} | = 4 | Z_{2} | . I f z = \frac{3 z_{1}}{2 z_{2}} + \frac{2 z_{2}}{3 z_{1}}$ then
A $| z | = \frac{1}{2} \sqrt{\frac{17}{2}}$
BIm(z)=0
CRe(z) =0
D $| z | = \sqrt{\frac{5}{2}}$

IIT JEE PREVIOUS YEAR-COMPLEX NUMBERS-TOPIC 3 ARGUMENT OF A COMPLEX NUMBER (OBJECTIVE QUESTIONS II)(ANALYTICAL & DESCRIPTIVE QUESTIONS )

Let z1=10+6i and z2=4+6idot If z is any complex number such that the a...
03:39

Home
Ask Doubt
Profile