A particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and a distance 2l apart. Prove that the motion of the particle will be SHM if it is displaced slightly along the line connecting them and released. Also find its time period.
√π3Mε0dQq
√(π2Mε0d3Qq)
√π3Mε0d3Qq
√π3Mε0Qqd3
The correct Answer is:c
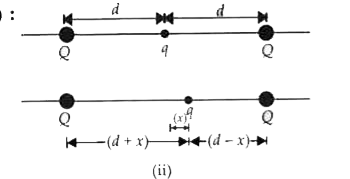
Let a charge q is displaced by x from the mean position as shown in the figure (ii).
The restoring force acting on the charge q to bring it in its mean position is
F=−[14πε0Q(d−x)2−14πε0Qq(d+x)2]
=−Qq4πε0[1(d−x)2−1(d+x)2]
=−Qq4πε0[(d+x)2−(d−x)2(d2−x2)2]=Qq4πε0[4dx(d2−x2)2]
Since x<<d
∴F=−Qq4πε0[4dxd4]=−Qqxπε0d3
Acceleration , a=FM=−Qqxπε0d3M ...(i)
As a∝−x
The charge will execute simple harmonic motion . The standard equation of SHM is
a=−ω2x (ii)
Comparing (i) and (ii) , we get
ω2=Qqπε0d3Morω√Qqπε0d3M
Time period , T=2πω=2π√πε0Md3Qq=2√π3ε0Md3Qd
Topper's Solved these Questions
- ELECTROSTATICSBook:MTG-WBJEEChapter:ELECTROSTATICSExercise:(WB JEE Previous Years Questions ) CATEGORY 3 : One or More than One Opion correct Type
Explore 4 Videos
- ELECTROSTATICSBook:MTG-WBJEEChapter:ELECTROSTATICSExercise:(WB JEE Previous Years Questions ) CATEGORY 1 : Single Option correct Type
Explore 23 Videos
- ELECTROMAGNETIC WAVES Book:MTG-WBJEEChapter:ELECTROMAGNETIC WAVES Exercise:WB JEE WORKOUT (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)
Explore 10 Videos
- GRAVITATIONBook:MTG-WBJEEChapter:GRAVITATIONExercise:WB JEE Previous Years Questions (CATEGORY 1: Single Option Correct Type
Explore 7 Videos
Similar Questions
A particle of mass m and charge +q is located midway between two fixed charged particles each having a charge +q and at a distance 2L apart. Assuming that the middle charge moves along the line joining the fixed charges, calculate the frequency of oscillation when it is displaced slightly.
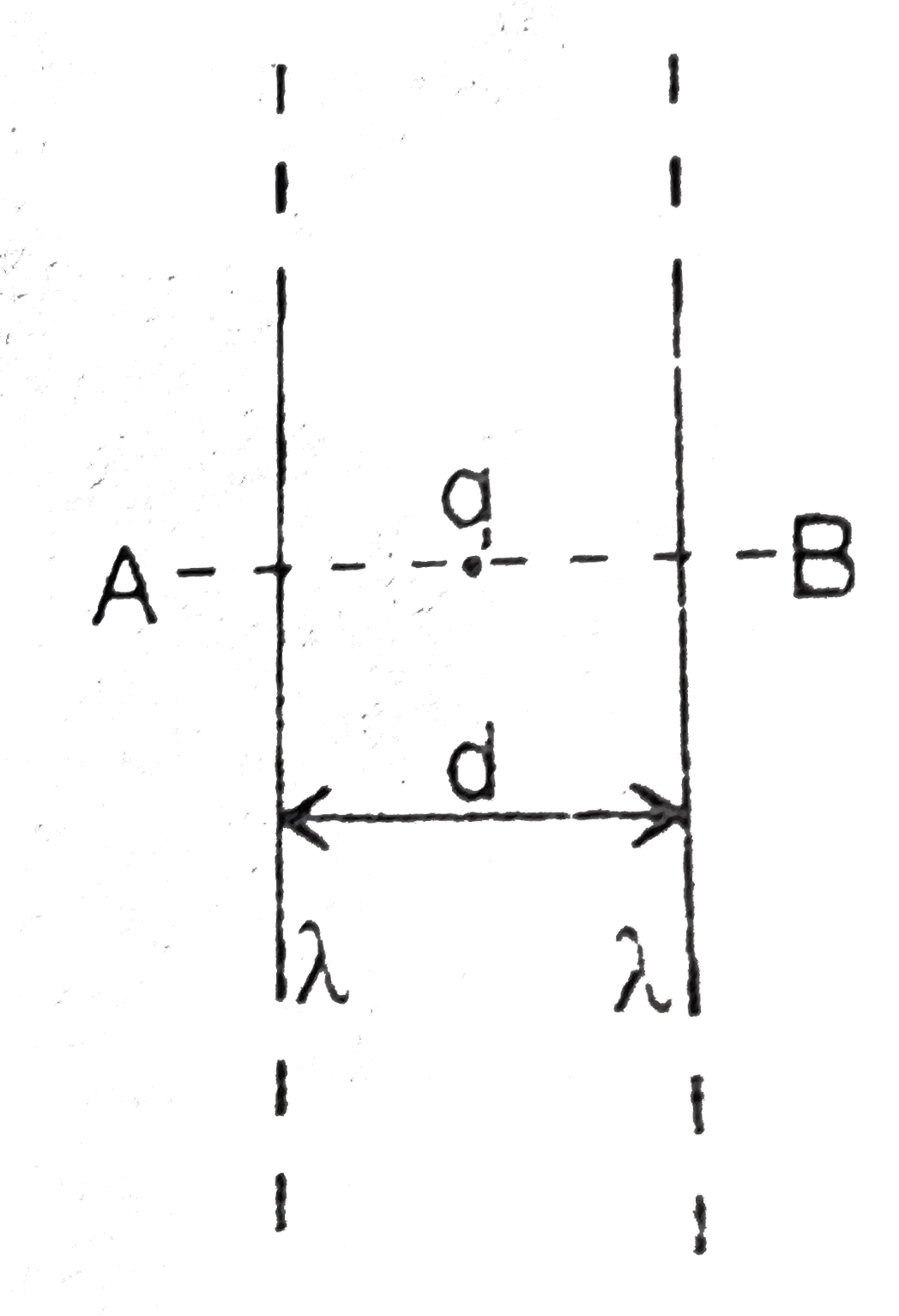
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
View Solution
Knowledge Check
A particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and at a distance 2L apart so that distance of this charge from each charge located at end is L. Assuming that the middle charge moves along the line joining the fixed charges. The frequency of oscillation when it is displaced slightly is
Aqπ√mπε0L3Bq4π(mπε0L3)C2qπ√mπε0L3Dq2π√mπε0L3A particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
Aq2EyBqEyCaE2yDqEy2Two positively charged particles each having charge Q and are d distance apart. A third charge is introduced in midway on the line joining the two charges. Find the nature and magnitude of third charge so that the system is in equilibrium.
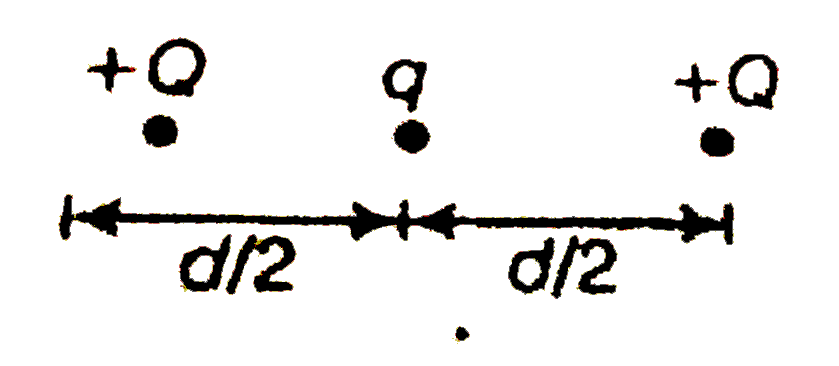 Aq=Q4Bq=Q4Cq=3Q4Dq=−3Q4
Aq=Q4Bq=Q4Cq=3Q4Dq=−3Q4
Two points charges , each Q , are fixed at separation 2d. A charged particle having charge q and mass m is placed between them.
(a) Now this charged particle is slightly displaced along the line joining the charges , slow that it will execute simple harmonic motion and find the time period of oscillation.
(b) If charge q is negative and it is displaced slightly perpendicular to the line joining the charges , repeat the part (a).
View SolutionA particle of mass m and charge -q moves along a diameter of a uniformluy charged sphere of radinus R and carrying a total charge +Q. Find the frequency of S.H.M. of the particle if the amplitude does not exceed .
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View SolutionA thin fixed ring of radius 'R' and positive charge 'Q' is placed in a vertical plane. A particle of mass 'm' and negative charge 'q' is placed at the centre of ring. If the particle is given a small horizontal displacement, show that it executes SHM. Also find the time period of small oscillations of this particle, about the centre of ring. (Ignore gravity)
View SolutionAs shown in the adjoining figure two charge particles each having charge q and mass m and d distance apart from each other. If two particle in equilibrium under the gravitational and electric force, then determine the ratio q/m.

View Solution