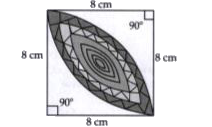
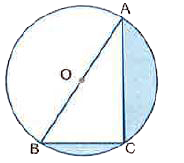
Calculate the area of the designed region in Fig. 12.29, which is compon between the two quadtants of circles of radius, 8 cm each.
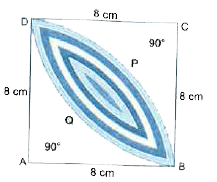
The correct Answer is:36.57cm2
Step by step video, text & image solution for Calculate the area of the designed region in Fig. 12.29, which is compon between the two quadtants of circles of radius, 8 cm each. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Long Answer Questions
13 Videos
- AREAS RELATED TO CIRCLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - HOTS (Higher Order Thinking Skills)
6 Videos
- AREAS RELATED TO CIRCLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Short Answer Questions -I
13 Videos
- ARITHMETIC PROGRESSIONS BOOK - VK GLOBAL PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - SELF ASSESSMENT TEST
10 Videos
Similar Questions
Knowledge Check
The area of the square inscribed in a circle of radius 8 cm is
A256 sq. cmB250 sq. cmC128sq. CmD125 sq. cm
Calculate the area of the designed region in fig. 15.55 common between two quadrilate of circles of radius 8 cm each.
View SolutionCalculate the area of the designed region in the given figure, common between two quadrants of circles of radius 7cm each.

View SolutionCalculate the area of the designed region in common between the two quadrants of circles of radius 8 cm each.
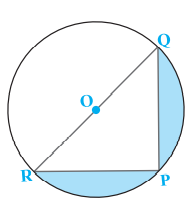
View SolutionFind the area of the shaded region in Fig. 12.19, if PQ=24 cm, PR=7 cm and O is the centre of the circle.
View SolutionFind the area of the shaded region in Fig. 12.20, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC=40∘
View SolutionFind the area of the shaded region in Fig. 15.29, where radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC=40o . (FIGURE)
View SolutionFind the area of the shaded region in Fig. 12.56, if AC= 24 cm, BC= 10 cm and O is the centre of the circle. (π=3.14)
View Solution