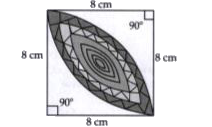
Calculate the area of the designed region in the given figure, common between two quadrants of circles of radius 7cm each.

Area of the designed region
=[ar(quadrantABCD)−ar(ΔABC)]
=2[14πx(7)2−12×7×7]cm2
=2[(14×227×49)−(492)]cm2
=2(772−492)cm2=(2×282)cm2=28cm2
Hence, the area of the designed region is 28cm2
Topper's Solved these Questions
- AREA OF CIRCLE, SECTOR AND SEGMENT Book:RS AGGARWALChapter:AREA OF CIRCLE, SECTOR AND SEGMENT Exercise:SOLVED EXAMPLE_TYPE
Explore 1 Video
- AREA OF CIRCLE, SECTOR AND SEGMENT Book:RS AGGARWALChapter:AREA OF CIRCLE, SECTOR AND SEGMENT Exercise:Exercise 16A
Explore 65 Videos
- ARITHMETIC PROGRESSIONBook:RS AGGARWALChapter:ARITHMETIC PROGRESSIONExercise:Multiple Choice Questions (Mcq)
Explore 30 Videos
Similar Questions
Knowledge Check
Find the area of shaded region in the given figure in which the squares is of side 100 cm and quadrant of radius 14 cm is formed and four corners.
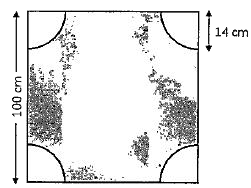 A9384 cm2B8998 cm2C9212 cm2D9656 cm2
A9384 cm2B8998 cm2C9212 cm2D9656 cm2
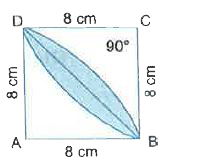
Calculate the area of the designed region in fig. 15.55 common between two quadrilate of circles of radius 8 cm each.
View SolutionCalculate the area of the designed region in common between the two quadrants of circles of radius 8 cm each.
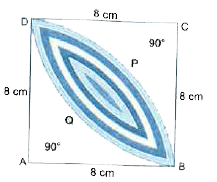
View SolutionCalculate the area of the designed region in Fig. 12.29, which is compon between the two quadtants of circles of radius, 8 cm each.
View SolutionCalculate the area of the shaded region in each of the figures given below:
View Solution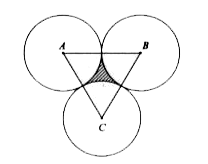
What is the area of the shaded region in the given figure, If the radius of each of the cirles is 2 cm ?
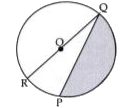
View SolutionFind the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
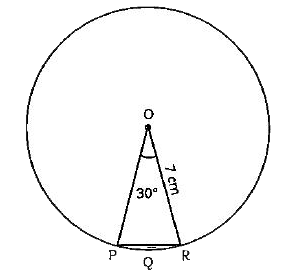
View SolutionWhat is the area of the segment PQR, in the given figure, if the radius of the circle is 7 cm?
(use π=227)
View Solution