A fire at the building B is reported by a telephone to two fire stations F1 and F2, 10 km apart from each other on a straight road. F1 and F2 observe that the fire is at an angle of 60∘ and 45∘ respectively to the road, which station should send its team and how much will it have to travel?
The correct Answer is:F1,13.66km
To solve the problem, we will use the concept of trigonometry, specifically the tangent function, to find the distances from the fire stations to the fire.
1. Understanding the Setup:
- Let the distance from fire station F1 to the fire be x km.
- Then, the distance from fire station F2 to the fire will be 10−x km since the two stations are 10 km apart.
2. Using the Angle from F2:
- From fire station F2, the angle of elevation to the fire is 45∘.
- Using the tangent function:
tan(45∘)=oppositeadjacent=ABBF2
- Since tan(45∘)=1:
1=AB10−x
- This implies:
AB=10−x(Equation 1)
3. Using the Angle from F1:
- From fire station F1, the angle of elevation to the fire is 60∘.
- Again using the tangent function:
tan(60∘)=ABBF1
- Since tan(60∘)=√3:
√3=ABx
- This implies:
AB=x√3(Equation 2)
4. Equating the Two Expressions for AB:
- From Equation 1 and Equation 2, we can set them equal to each other:
10−x=x√3
- Rearranging gives:
10=x√3+x
- Factoring out x:
10=x(√3+1)
- Solving for x:
x=10√3+1
5. Rationalizing the Denominator:
- To simplify x:
x=10(√3−1)(√3+1)(√3−1)=10(√3−1)3−1=5(√3−1)
- Approximating √3≈1.732:
x≈5(1.732−1)≈5(0.732)≈3.66 km
6. Finding the Distance from F2:
- The distance from F2 to the fire is:
10−x=10−3.66≈6.34 km
7. Conclusion:
- Since x≈3.66 km, fire station F1 is closer to the fire.
- Therefore, F1 should send its team, and it will have to travel approximately 3.66 km.
- Let the distance from fire station F1 to the fire be x km.
- Then, the distance from fire station F2 to the fire will be 10−x km since the two stations are 10 km apart.
- From fire station F2, the angle of elevation to the fire is 45∘.
- Using the tangent function:
tan(45∘)=oppositeadjacent=ABBF2
- Since tan(45∘)=1:
1=AB10−x
- This implies:
AB=10−x(Equation 1)
- From fire station F1, the angle of elevation to the fire is 60∘.
- Again using the tangent function:
tan(60∘)=ABBF1
- Since tan(60∘)=√3:
√3=ABx
- This implies:
AB=x√3(Equation 2)
- From Equation 1 and Equation 2, we can set them equal to each other:
10−x=x√3
- Rearranging gives:
10=x√3+x
- Factoring out x:
10=x(√3+1)
- Solving for x:
x=10√3+1
- To simplify x:
x=10(√3−1)(√3+1)(√3−1)=10(√3−1)3−1=5(√3−1)
- Approximating √3≈1.732:
x≈5(1.732−1)≈5(0.732)≈3.66 km
- The distance from F2 to the fire is:
10−x=10−3.66≈6.34 km
- Since x≈3.66 km, fire station F1 is closer to the fire.
- Therefore, F1 should send its team, and it will have to travel approximately 3.66 km.
Topper's Solved these Questions
- HEIGHT AND DISTANCEBook:VK GLOBAL PUBLICATIONChapter:HEIGHT AND DISTANCEExercise:PROFICIENCY EXERCISE ( LONG ANSWER QUESTIONS II)
Explore 11 Videos
- COORDINATE GEOMETRY Book:VK GLOBAL PUBLICATIONChapter:COORDINATE GEOMETRY Exercise:SELF-ASSESSMENT TEST
Explore 10 Videos
- INTRODUCTION TO TRIGONOMETRYBook:VK GLOBAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRYExercise:SELF - ASSESSMENT TEST
Explore 9 Videos
Similar Questions
A fire in building B is reported on telephone to two fire stations P and O, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60 degree to the road and Q observes it an angle of 45 degrees to the road. Which station should send its team and how much will the team have to travel?
View SolutionA fire in a building B is reported on telephone to two fire stations P and Q , 20km apart from each other on a straight road. P observes that the fire is at an angle of 60o to the road and Q observes that it is at an angle of 45o to the road. Which station should send its team and how much will this team have to travel?
View Solution
Knowledge Check
A particle is observed from two frames S1andS2. The frame S2 moves with respect to S1 with an acceleration a. Let F1andF2 be the pseudo forces on the particle when seen from S1andS2 respectively. Which of the following are not possible ?
AF1≠0,F2=0BF1≠0,F2≠0CF1=0,F2≠0DF1=0,F2=0Two forces −→F1and−→F2 are acting at right angles to each other , find their resultant ?
A√F21−F22B√F21+F22C√(F1+F2)DF1+F2In the figure, blocks A, B and C of mass m each have acceleration a1, a2 and a3 respectively. F1 and F2 are external forces of magnitudes 2mg and mg respectively, then :
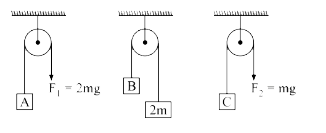 Aa1=a2=a3Ba1>a2>a3Ca1=a2,a2>a3Da1>a2,a2=a3
Aa1=a2=a3Ba1>a2>a3Ca1=a2,a2>a3Da1>a2,a2=a3
Draw a circle ofradius 4 cm. Draw two tangents to the circle inclined at an angle of 60∘ to each other.
View SolutionDraw a circle ofradius 4 cm. Draw two tangents to the circle inclined at an angle of 60∘ to each other.
View SolutionA fire at a building A is reported on telephone to two fire stations F1 and F2, 10 km apart from each other on a straight road. F1 observes that the fire is at an angle of 60∘ to the road and F2 observes that it is at angle of 45∘omit.Aord∈g→decisionbyhigherauthoritystationF_1 sends its team.
) Which value is depicted in the decision of higher authority?
View SolutionTwo stations A and B are 500 km away. If two buses each start from station A and B simultaneously travelling towards the other station with speeds 80 km/h and 90 km/h , respectively, find the distance between the two buses exactly after 2 h.
View SolutionA body is acted upon by two forces of manitudes F1=√2NandF2=3N which are inclined at 45∘ to each other. There magnitude of resultant force acting on the body is
View Solution

