The angles of depression of two ships from the top of a light house are 45∘ and 30∘ towards east. If the ships are 200 m apart, find the height of light house.
The correct Answer is:273m
To solve the problem, we need to find the height of the lighthouse based on the angles of depression to two ships that are 200 meters apart. Let's denote the height of the lighthouse as h.
Step 1: Understanding the Angles of Depression
The angle of depression from the top of the lighthouse to the ships is given as 45∘ for the first ship (let's call it Ship A) and 30∘ for the second ship (let's call it Ship B).
Step 2: Drawing the Diagram
We can visualize the situation by drawing a right triangle for each ship. The height of the lighthouse is the vertical side of the triangle, and the horizontal distance from the base of the lighthouse to each ship is the horizontal side.
Step 3: Setting Up the Right Triangles
1. For Ship A (angle of depression 45∘):
- Using the tangent function:
tan(45∘)=hd1
Since tan(45∘)=1:
h=d1
2. For Ship B (angle of depression 30∘):
- Using the tangent function:
tan(30∘)=hd2
Since tan(30∘)=1√3:
1√3=hd2⟹d2=h√3
Step 4: Relating the Distances
The distance between the two ships is given as 200 meters. Therefore, we can express this relationship as:
d2−d1=200
Substituting the expressions for d1 and d2:
h√3−h=200
Step 5: Simplifying the Equation
Factoring out h:
h(√3−1)=200
Step 6: Solving for h
Now, we can solve for h:
h=200√3−1
Step 7: Rationalizing the Denominator
To simplify further, we can rationalize the denominator:
h=200(√3+1)(√3−1)(√3+1)=200(√3+1)3−1=200(√3+1)2=100(√3+1)
Step 8: Final Calculation
Now we can calculate the approximate value of h:
h≈100(1.732+1)≈100(2.732)≈273.2 meters
Thus, the height of the lighthouse is approximately 273.2 meters.
---
The angle of depression from the top of the lighthouse to the ships is given as 45∘ for the first ship (let's call it Ship A) and 30∘ for the second ship (let's call it Ship B).
We can visualize the situation by drawing a right triangle for each ship. The height of the lighthouse is the vertical side of the triangle, and the horizontal distance from the base of the lighthouse to each ship is the horizontal side.
1. For Ship A (angle of depression 45∘):
- Using the tangent function:
tan(45∘)=hd1
Since tan(45∘)=1:
h=d1
- Using the tangent function:
tan(30∘)=hd2
Since tan(30∘)=1√3:
1√3=hd2⟹d2=h√3
The distance between the two ships is given as 200 meters. Therefore, we can express this relationship as:
d2−d1=200
Substituting the expressions for d1 and d2:
h√3−h=200
Factoring out h:
h(√3−1)=200
Now, we can solve for h:
h=200√3−1
To simplify further, we can rationalize the denominator:
h=200(√3+1)(√3−1)(√3+1)=200(√3+1)3−1=200(√3+1)2=100(√3+1)
Now we can calculate the approximate value of h:
h≈100(1.732+1)≈100(2.732)≈273.2 meters
Topper's Solved these Questions
- HEIGHT AND DISTANCEBOOK - VK GLOBAL PUBLICATIONCHAPTER - HEIGHT AND DISTANCEEXERCISE - PROFICIENCY EXERCISE ( LONG ANSWER QUESTIONS II)
11 Videos
- COORDINATE GEOMETRY BOOK - VK GLOBAL PUBLICATIONCHAPTER - COORDINATE GEOMETRY EXERCISE - SELF-ASSESSMENT TEST
10 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - VK GLOBAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - SELF - ASSESSMENT TEST
9 Videos
Similar Questions
The angles of depresion of two ships from the top of a lighthouse are 45∘ and 30∘ towards east. If the ships are 100 m apart, find the height of the lighthouse.
View SolutionThe angles of depression of two ships from the top of a light house are 45∘and30∘ towards east. If the ships are 200 m apart, the height of the light house is : (Take √3=1.73)
View Solution
Knowledge Check
The angles of depression from the top of a light house of two boats are 45∘and30∘ towards the west. If the two boats are 5m apart, then the heighat of the light house is
A(2.5V3 -1)mB2.5 (V3 -1)mC(2.5 V 3 + 1)mD2.5 (V3 + 1) mAngle of depression from the top of a light house of two boats are 45∘and30∘ due east which are 60 m apart. The height of the light house is
A60√3B30(√3+1)C30(√3−1)DNoneTwo ships A and B are sailing straight away from the foot of a tower OP along routes such that ∣AOB––––––– is always 120∘. At a certain instance, the angles of depression of the ships A and B from the top P of the towers are 60∘and30∘ respectively. The distance between the ships when the height of the tower is 15m is
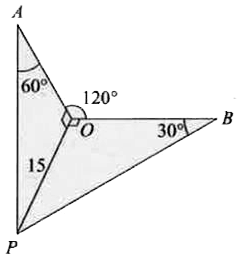 A5√39 mB5√30 mC5√21 mD5√3 m
A5√39 mB5√30 mC5√21 mD5√3 m
The angles of depression of two ships from the top of a light house are 60∘ and 45∘ towards east. If the ships are 300 m apart, the height of the light house is
किसी प्रकाश स्तंभ के शीर्ष भाग से दो पत्तो के अवनमन कोण पूर्व की ओर 60∘ और 45∘ है। यदि पोत परस्पर 300 मीटर की दूरी पर हो, तो प्रकाश स्तंभ को ऊँचाई बताइए?
View SolutionThe angles of depression of two ships from the top of a light house are 45o and 30o towards east. If the ships are 100 m apart, the height of the light house is 50√3+1m (b) 50√3−1m (c) 50(√3−1)m (d) 50(√3+1)m
View SolutionThe angles of depression of two ships from the top of a lighthouse are 45∘and30∘. If the ships are 120 m apart, then find the height of the lighthouse.
View SolutionThe angles of depression of two ships from the top of a light house and on the same side of it are found to be 45o and 30o respectively. If the ships are 200m apart, find the height of the light house.
View SolutionTwo ships are sailing in the sea on the either side of the lighthouse.The angles of depression of two ships as observed from the top of the lighthouse are 60∘ and 45∘, respectively. If the distance between the ships is 100(√3+1√3) m, then find the height of the lighthouse
View Solution
