Find the length of the the tangent from the external point P at a distance of 20 cm from the centre of a circle of radius 12 cm.
The correct Answer is:16 cm
To find the length of the tangent from the external point P to the circle, we can use the Pythagorean theorem. Here’s a step-by-step solution:
Step 1: Identify the given values
- Distance from the center of the circle (O) to the external point (P): OP=20 cm
- Radius of the circle (OA): OA=12 cm
Step 2: Understand the relationship in the triangle
When a tangent is drawn from an external point to a circle, it forms a right triangle with the radius and the line connecting the center of the circle to the external point. In this triangle:
- OP is the hypotenuse,
- OA is one leg (the radius),
- AP is the other leg (the length of the tangent we want to find).
Step 3: Apply the Pythagorean theorem
According to the Pythagorean theorem:
OP2=OA2+AP2
Substituting the known values:
202=122+AP2
Step 4: Calculate the squares
Calculating the squares:
400=144+AP2
Step 5: Rearrange the equation to solve for AP2
Subtract 144 from both sides:
AP2=400−144
AP2=256
Step 6: Take the square root to find AP
Now, take the square root of both sides:
AP=√256
AP=16 cm
Final Answer
The length of the tangent from the external point P is 16 cm.
---
- Distance from the center of the circle (O) to the external point (P): OP=20 cm
- Radius of the circle (OA): OA=12 cm
When a tangent is drawn from an external point to a circle, it forms a right triangle with the radius and the line connecting the center of the circle to the external point. In this triangle:
- OP is the hypotenuse,
- OA is one leg (the radius),
- AP is the other leg (the length of the tangent we want to find).
According to the Pythagorean theorem:
OP2=OA2+AP2
Substituting the known values:
202=122+AP2
Calculating the squares:
400=144+AP2
Subtract 144 from both sides:
AP2=400−144
AP2=256
Now, take the square root of both sides:
AP=√256
AP=16 cm
The length of the tangent from the external point P is 16 cm.
Topper's Solved these Questions
- CIRCLES Book:VK GLOBAL PUBLICATIONChapter:CIRCLES Exercise:PROFICIENCY EXERCISE (Short Answer Questions - II 3 mark)
Explore 22 Videos
- CIRCLES Book:VK GLOBAL PUBLICATIONChapter:CIRCLES Exercise:PROFICIENCY EXERCISE (Long Answer Questions 4 mark)
Explore 12 Videos
- CIRCLES Book:VK GLOBAL PUBLICATIONChapter:CIRCLES Exercise:PROFICIENCY EXERCISE (Very Short Answer Questions 1 mark)
Explore 13 Videos
- ARITHMETIC PROGRESSIONS Book:VK GLOBAL PUBLICATIONChapter:ARITHMETIC PROGRESSIONS Exercise:SELF ASSESSMENT TEST
Explore 10 Videos
- COORDINATE GEOMETRY Book:VK GLOBAL PUBLICATIONChapter:COORDINATE GEOMETRY Exercise:SELF-ASSESSMENT TEST
Explore 10 Videos
Similar Questions
Find the length of the tangent segment from a point which is at a distance of 5 cm from the centre of the circle of radius 3cm.
View SolutionFind the distance of a chord of length 12 cm from the centre of a circle of radius 10 cm.
View SolutionThe length of tangent from a point A at a distance of 12 cm from the centre of the circle is 9 cm. What is the radius of the circle ?
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm . Find the radius of the circle.
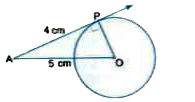
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
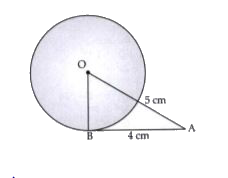
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
View SolutionThe length of tangent from a point A at a distance of 5 cm from the centre of the circle is 4 cm. What will be the radius of the circle ?
View SolutionFind the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
View SolutionFind the length of tangent drawn to a circle of radius 6 cm, from a point at a distance of 10 cm from the centre.
View SolutionThe length of the tangent drawn from a point 8 cm away from the centre of a circle of radius 6 cm is .
View Solution