Two batteries of difference emf's and internal resistance are connected in parallel to one another.
Equivalent emf will be grater than either of the emf's
Equivalent emf will be smaller than either of the emf
Equivalent internal resistance will be grater than either of the two internal resistances
Equivalent internal resistance will be smaller than either of the two internal resistances.
The correct Answer is:D
To solve the problem of two batteries with different EMFs and internal resistances connected in parallel, we will analyze the situation step by step.
Step 1: Identify the parameters of the batteries
Let’s denote the EMFs and internal resistances of the two batteries as follows:
- Battery 1: EMF = E1, Internal Resistance = R1
- Battery 2: EMF = E2, Internal Resistance = R2
Step 2: Understand the configuration
The two batteries are connected in parallel. In a parallel connection, the voltage across each battery is the same, and the total current flowing through the circuit is the sum of the currents from each battery.
Step 3: Analyze the equivalent EMF
When two batteries are connected in parallel, the equivalent EMF (E_eq) is determined by the battery with the higher EMF. However, the actual voltage across the terminals will be affected by the internal resistances and the current flowing through the circuit.
Using Kirchhoff's Voltage Law (KVL), we can express the voltage across the terminals:
- For Battery 1: V=E1−I⋅R1
- For Battery 2: V=E2−I⋅R2
Since both batteries are in parallel, the voltage across them must be equal:
E1−I1⋅R1=E2−I2⋅R2
Step 4: Determine the equivalent EMF
To find the equivalent EMF, we note that the current will flow from the battery with the higher EMF to the one with the lower EMF. Therefore, if E1 > E2, the equivalent EMF will be less than E1 and E2 due to the voltage drop across the internal resistances.
Thus, we can conclude:
- The equivalent EMF (E_eq) will be less than the higher EMF (E1 or E2).
Step 5: Analyze the equivalent internal resistance
The equivalent internal resistance (R_eq) of two resistors in parallel is given by the formula:
Req=R1⋅R2R1+R2
This formula shows that the equivalent resistance will always be less than either of the individual resistances (R1 or R2).
Conclusion
From our analysis, we can summarize:
1. The equivalent EMF (E_eq) will be less than either of the individual EMFs (E1 or E2).
2. The equivalent internal resistance (R_eq) will be less than either of the internal resistances (R1 or R2).
Final Answer
- The equivalent EMF is less than either of the two EMFs.
- The equivalent internal resistance is smaller than either of the two internal resistances.
Let’s denote the EMFs and internal resistances of the two batteries as follows:
- Battery 1: EMF = E1, Internal Resistance = R1
- Battery 2: EMF = E2, Internal Resistance = R2
The two batteries are connected in parallel. In a parallel connection, the voltage across each battery is the same, and the total current flowing through the circuit is the sum of the currents from each battery.
When two batteries are connected in parallel, the equivalent EMF (E_eq) is determined by the battery with the higher EMF. However, the actual voltage across the terminals will be affected by the internal resistances and the current flowing through the circuit.
- For Battery 1: V=E1−I⋅R1
- For Battery 2: V=E2−I⋅R2
E1−I1⋅R1=E2−I2⋅R2
To find the equivalent EMF, we note that the current will flow from the battery with the higher EMF to the one with the lower EMF. Therefore, if E1 > E2, the equivalent EMF will be less than E1 and E2 due to the voltage drop across the internal resistances.
- The equivalent EMF (E_eq) will be less than the higher EMF (E1 or E2).
The equivalent internal resistance (R_eq) of two resistors in parallel is given by the formula:
Req=R1⋅R2R1+R2
From our analysis, we can summarize:
1. The equivalent EMF (E_eq) will be less than either of the individual EMFs (E1 or E2).
2. The equivalent internal resistance (R_eq) will be less than either of the internal resistances (R1 or R2).
- The equivalent EMF is less than either of the two EMFs.
- The equivalent internal resistance is smaller than either of the two internal resistances.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION FOR COMPETITIVE EXAMINATIONS)
Explore 20 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
Explore 45 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:REVISION EXERCISES (NUMERICAL PROBLEMS)
Explore 24 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
Two batteries of different emfs and different internal resistances are connected as shown. The voltage across AB in volts is.
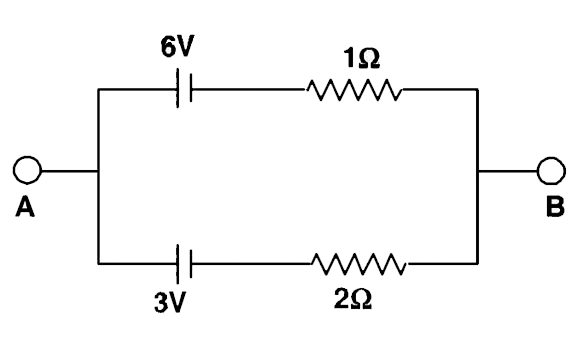 .
.
View SolutionTwo batteries each of emf ε and internal resistance r, are connected in parallel. If we take current from this combination in a external resistance R, then for what value of R maximum power will beobtained? What will be this power?
View Solution
Knowledge Check
Two batteries of different emf and internal resistances connected in series with each other and with an external load resistor. The current reversed, the current becomes 1.0 A. the ratio of the emf of the two batteries is
A2.5:1B2:1C3:2D1:1A cell of emf (E) and internal resistance (r) is balanced across (l) length of potentiometer wire. If another cell of emf 2E and internal resistance (2r) is connected in parallel to the first cell , then the balancing length will be
A1/3B21/3C41/3D21If n cells each of emf E and internal resistance are connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr
Two batteries each of emf ε and internal resistance r, are connected in parallel. If we take current from this combination in a external resistance R, then for what value of R maximum power will beobtained? What will be this power?
View SolutionA battery of emf 6 volts and internal resistance 1Ω is connected in parallel to another battery of emf 8V and internal resistance 2Ω. The combination is then used to send current through an external resistance of 10Ω. Find the current through the external resistance.
View SolutionA : When two cells of equal EMF and equal internal resistances are connected is parallel with positive plate of the other than , the net EMF , of the combination will be equal to the EMF of each cell.
R : Effective internal resistance of the parallel combination of two identical cells will be half of the internal resistance of each cell.
View SolutionTwo batteries, one of emf 18 V and internal resistance 2 Ω and the other of emf 12 V and internal resistance 1Ω , are connected in parallel as shown in Fig. The voltmeter V will record a reading of

View SolutionTwo batteries each of E and internal resistance r are connected turn by turn in series and in parallel, and are used to find current in an external resistance R. If the current in series is equal to that in parallel, the internal resistance of each battery is
View Solution

