Inductance L is 230 mH and the sinusoidal alternating emf device operates at amplitude Em =36.0 V and frequency fd=60.0 Hz.
(a) What are the potential difference vL(t) across the inductance and the amplitude VL of vL(t) ?
To solve the problem, we need to find the potential difference vL(t) across the inductance and the amplitude VL of vL(t).
Step 1: Understand the given values
We are given:
- Inductance L=230mH=0.230H
- Amplitude of the emf Em=36.0V
- Frequency fd=60.0Hz
Step 2: Calculate the angular frequency ω
The angular frequency ω is calculated using the formula:
ω=2πf
Substituting the given frequency:
ω=2π×60.0Hz=120πrad/s
Step 3: Write the expression for the emf E(t)
The emf as a function of time can be expressed as:
E(t)=Emsin(ωt)
Substituting the amplitude:
E(t)=36.0sin(120πt)V
Step 4: Determine the potential difference vL(t)
In a purely inductive circuit, the potential difference across the inductor vL(t) is given by:
vL(t)=LdI(t)dt
However, since we are interested in the relationship between voltage and current in an inductor, we can directly relate it to the emf:
vL(t)=E(t)=36.0sin(120πt)V
Step 5: Find the amplitude VL
The amplitude VL of the potential difference vL(t) is simply the maximum value of the sinusoidal function:
VL=Em=36.0V
Final Answers
- The potential difference vL(t) across the inductance is:
vL(t)=36.0sin(120πt)V
- The amplitude VL of vL(t) is:
VL=36.0V
We are given:
- Inductance L=230mH=0.230H
- Amplitude of the emf Em=36.0V
- Frequency fd=60.0Hz
The angular frequency ω is calculated using the formula:
ω=2πf
Substituting the given frequency:
ω=2π×60.0Hz=120πrad/s
The emf as a function of time can be expressed as:
E(t)=Emsin(ωt)
Substituting the amplitude:
E(t)=36.0sin(120πt)V
In a purely inductive circuit, the potential difference across the inductor vL(t) is given by:
vL(t)=LdI(t)dt
However, since we are interested in the relationship between voltage and current in an inductor, we can directly relate it to the emf:
vL(t)=E(t)=36.0sin(120πt)V
The amplitude VL of the potential difference vL(t) is simply the maximum value of the sinusoidal function:
VL=Em=36.0V
- The potential difference vL(t) across the inductance is:
vL(t)=36.0sin(120πt)V
- The amplitude VL of vL(t) is:
VL=36.0V
Topper's Solved these Questions
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Check Point
8 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Problems
30 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
- ELECTROMAGNETIC WAVES BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
Capacitance C is 15.0 μF and the sinusoidal alternating emf device operates at amplitude Em = 36.0 V and frequency fd= 60.0 Hz.
(a) What are the potential difference VC(t) across the capacitance and the amplitude VC of Vc(t) ? (b) What are the current IC(t) in the circuit as a function of time and the amplitude IC of Ic(t) ?
View SolutionResistance R is 200 Ω and the sinusoidal alternating emf device operates at amplitude Em=36.0 V and frequency fd=60.0 Hz.
(a) What is the potential difference vR(t) across the resistance as a function of time t, and what is the amplitude VR of VR(t) ? (b)What is the current vR(t) in the resistance and the amplitude IR of IR(t) ?
View Solution
Knowledge Check
An alternating voltage is connected in series with a resistance R and inductance L if the potential drop across the resistance is 200V and across the inductance is 150V, then the applied voltage is
A350VB250VC500VD300VIn figure i1=10e−2tA,i2=4A,vC=3e−2tV
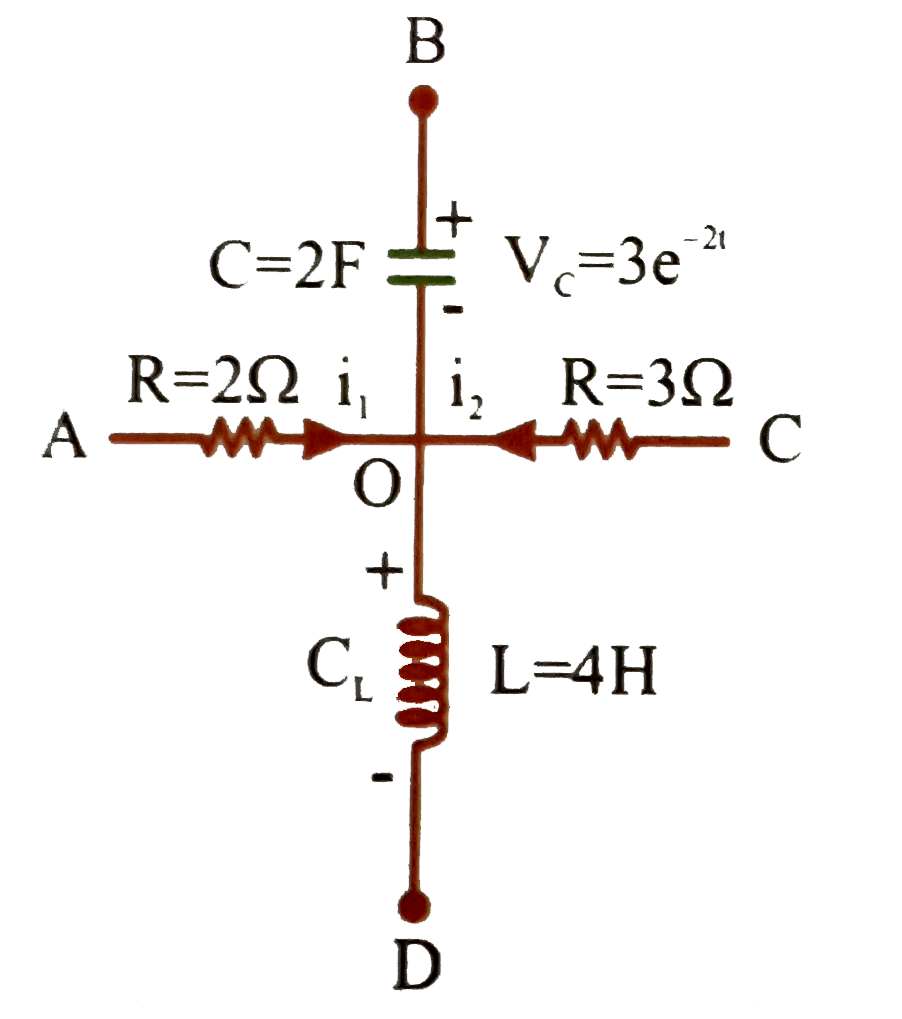
The potential difference across inductor VL is :A8e−2tVB9e−2tVC16e−2tVD18e−2tVAn alternating e.m.f. of 100V (rms) is applied to a series LCR circuit. At resonance, the potential difference across the inductance and across the capacitance is 400V each. The potential difference across the resistance will be
A100VB400VC800VDzero
An inductor of inductance 1 H is connected across an A C supply . The current in the circuit is a sinusoidal function of time with amplitude 0.5 A and frequency 50 Hz. Calculate the effective potential difference across the inductor .
View SolutionAn alternating source drives a series RLC circuit with an emf amplitude of 6.00 V, at a phase angle of +30.0∘. When the potential difference across the capacitor reaches its maximum positive value of +5.00 V, what is the potential difference across the inductor (sign included)?
View SolutionIn Fig. R = 25.0 Ω, C = 4.70 μF, and L = 25.0 mH. The generator provides an emf with rms voltage 75.0 V and frequency 550 Hz. (a) What is the rms current? What is the rms voltage across (b) R, (c) C, (d) L, (e) C and L together, and (f) R, C, and L together? At what average rate is energy dissipated by (g) R, (h) C, and (i) L?
View SolutionIn the circuit shown in figure, E=120V,R1=30.0Ω,R2=50.0Ω and L=0.200H. Switch S is closed at t=0. Just after the switch is closed.
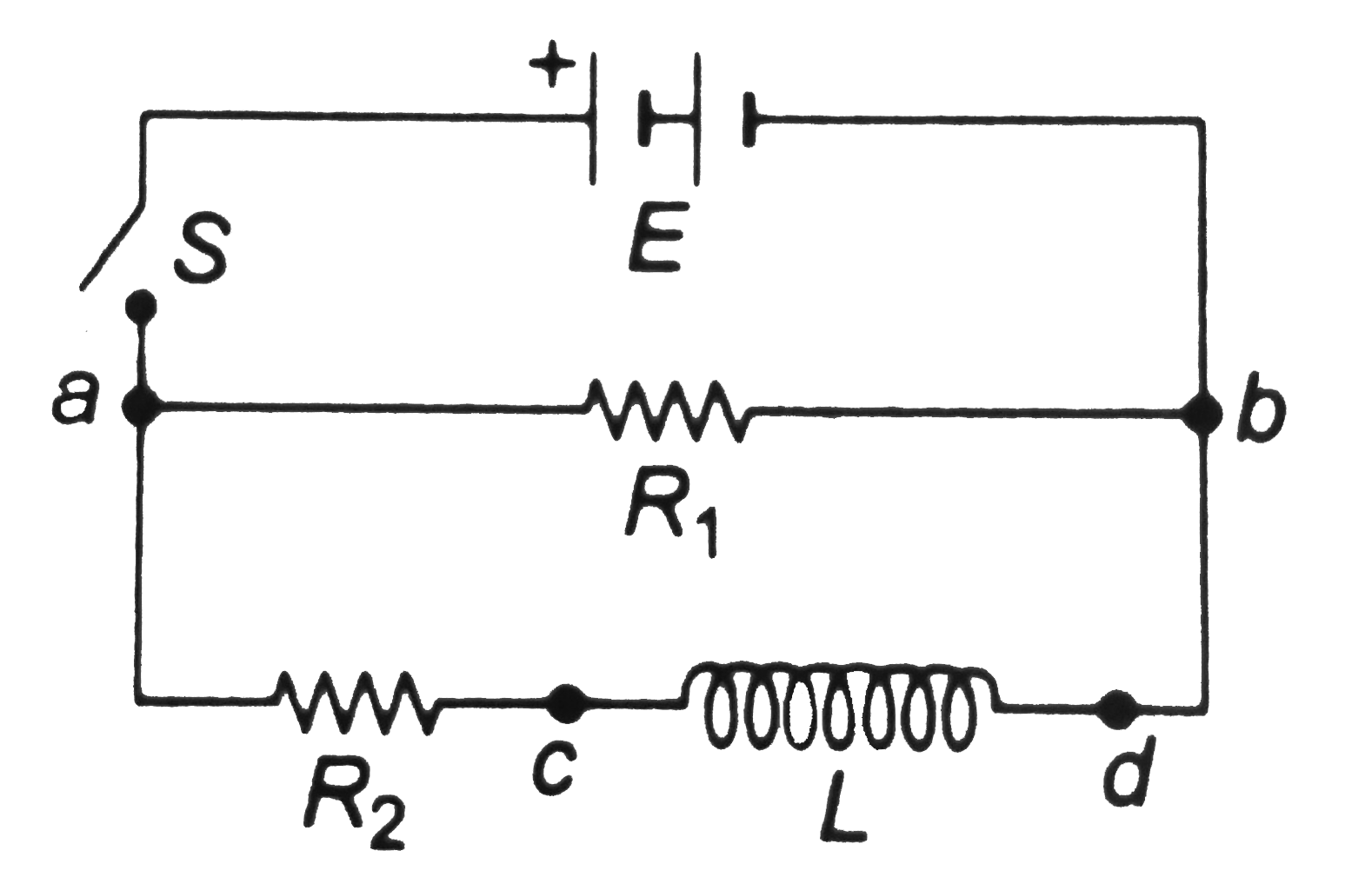
(a) What is the potential difference Vab across the inductor R1?
(b) Which point, a or b, is at higher potential?
(c) What is the potential difference Vcd across the inductor L?
(d) Which point, c or d, is at a higher potential? The switch is left closed for a long time and then is opened. Just after the switch is opened
(e) What is the potential difference Vab across the resistor R1?
(f) Which point a or b, is at a higher potential?
(g) What is the potential difference Vcd across the inductor L?
(h) Which point, c or d, is at a higher potential?
View SolutionAn alternating e.m.f. of 0.1 V is applied across an LCR series circuit having R=2Ω,C=40μFandL=100mH. At resonance, the voltage drop across the inductor is
View Solution
