A particle of mass 12g and charge 80μC moves through a uniform magnetic field, in a region where the free - fall acceleration is −9.8ˆjm/s2. The velocity of the particle is a constant 20ˆikm/s, which is perpendicular to the magnetic field. What then is the magnetic field ?
To solve the problem, we need to find the magnetic field B acting on a charged particle moving through it. Here's a step-by-step breakdown of the solution:
Step 1: Identify the given values
- Mass of the particle, m=12g=12×10−3kg
- Charge of the particle, q=80μC=80×10−6C
- Velocity of the particle, v=20km/s=20×103m/s in the direction of ^i
- Acceleration due to gravity, g=−9.8^jm/s2
Step 2: Write down the force acting on the particle
The force acting on a charged particle moving in a magnetic field is given by the equation:
F=qv×B
Since the particle is in free fall, the gravitational force acting on it can be expressed as:
Fgravity=mg=m(−9.8^j)=−9.8m^j
Step 3: Set the magnetic force equal to the gravitational force
For the particle to move with constant velocity (i.e., no acceleration), the magnetic force must balance the gravitational force:
qv×B=−mg
Step 4: Calculate the magnitude of the magnetic field
From the equation above, we can express the magnitude of the magnetic field B as:
B=maqv
Where a=9.8m/s2 (the magnitude of the gravitational acceleration).
Substituting the values:
B=(12×10−3kg)(9.8m/s2)(80×10−6C)(20×103m/s)
Step 5: Perform the calculation
Calculating the numerator:
12×10−3×9.8=0.1176kg m/s2
Calculating the denominator:
80×10−6×20×103=1.6C m/s
Now substituting these values into the equation for B:
B=0.11761.6=0.0735T
Step 6: Determine the direction of the magnetic field
Using the right-hand rule, if the velocity v is in the direction of ^i and the magnetic force F must counteract the gravitational force (downward), the magnetic field B must point in the negative z-direction (i.e., −^k).
Final Answer
Thus, the magnetic field is:
B=−0.0735^kT
- Mass of the particle, m=12g=12×10−3kg
- Charge of the particle, q=80μC=80×10−6C
- Velocity of the particle, v=20km/s=20×103m/s in the direction of ^i
- Acceleration due to gravity, g=−9.8^jm/s2
The force acting on a charged particle moving in a magnetic field is given by the equation:
F=qv×B
Since the particle is in free fall, the gravitational force acting on it can be expressed as:
Fgravity=mg=m(−9.8^j)=−9.8m^j
For the particle to move with constant velocity (i.e., no acceleration), the magnetic force must balance the gravitational force:
qv×B=−mg
From the equation above, we can express the magnitude of the magnetic field B as:
B=maqv
Where a=9.8m/s2 (the magnitude of the gravitational acceleration).
B=(12×10−3kg)(9.8m/s2)(80×10−6C)(20×103m/s)
Calculating the numerator:
12×10−3×9.8=0.1176kg m/s2
80×10−6×20×103=1.6C m/s
B=0.11761.6=0.0735T
Using the right-hand rule, if the velocity v is in the direction of ^i and the magnetic force F must counteract the gravitational force (downward), the magnetic field B must point in the negative z-direction (i.e., −^k).
Thus, the magnetic field is:
B=−0.0735^kT
Topper's Solved these Questions
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Single correct Choice Type )
24 Videos
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (More than one correct choice Type)
11 Videos
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Check point
6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )
3 Videos
Similar Questions
Knowledge Check
Particles 1, 2 and 3 are moving perpendicular to a uniform magnetic field, then particle
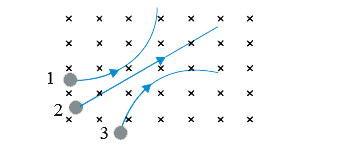 A1 is positively charged and particle 3 is negatively chargedB1 is negatively charged and particle 3 is positively chargedC1 is negatively charged and particle 2 is neutralD1 and 3 are positively charged and particle 2 is neutral
A1 is positively charged and particle 3 is negatively chargedB1 is negatively charged and particle 3 is positively chargedC1 is negatively charged and particle 2 is neutralD1 and 3 are positively charged and particle 2 is neutralA charged particle moves through a magnetic field perpendicular to its direction. Then
AAcceleration remain unchangedBvelocity remains unchangedCspeed of the particle remains unchangedDDirection of the particle remains unchangedA charge particle is moving in a plane perpendicular to uniform magnetic field, then
AIts momentum changes but kinetic energy remains the sameBBoth momentum and kinetic energy remain the sameCBoth will changeDKinetic energy change but momentum remains the same
A charged particle moves through a region of uniform magnetic field perpendicularly, Is the momentum of particle affected?
View SolutionA charged particle moves through a magnetic field perpendicular to its direction. Then
View SolutionA charged particle moves through a magnetic field perpendicular to its direction. Then
View SolutionA charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
View SolutionA charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
View Solution
