Question

A strong magnet is placed under a horizontal conducting ring of radius r that carries current i as shown in Fig. If the magnetic field makes an angle $\theta$ with the vertical at the ring's location, what are the magnitude and direction of the resultant force on the ring?

Explanation

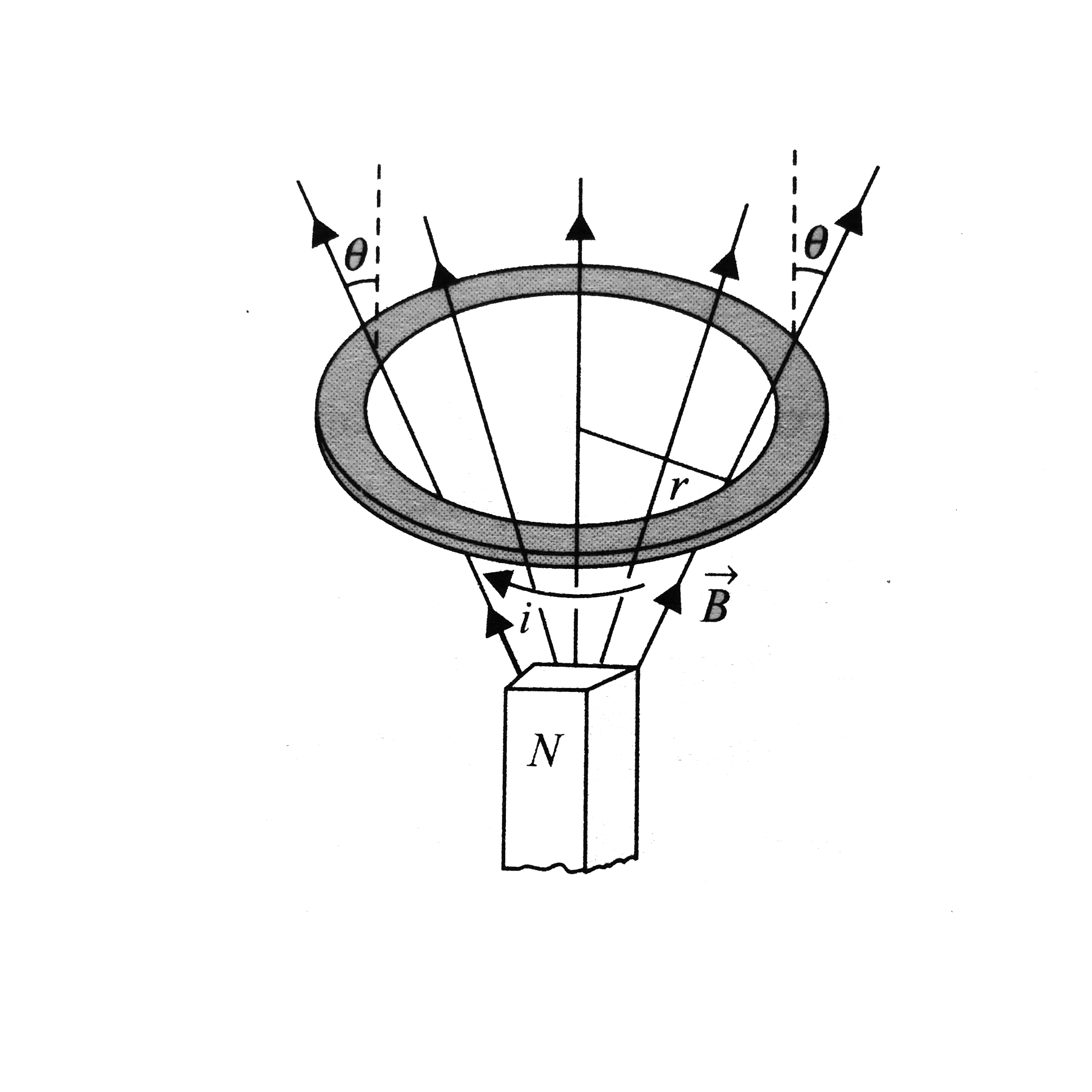
Here the wire is in a non-uniform magnetic field. The magnitude of the magnetic field at all the points of the ring is the same, but the direction is different. So, we can not say that the net force on wire is zero. We have two options: we can either divide the entire ring into small elements and integrate to find the force on the ring or

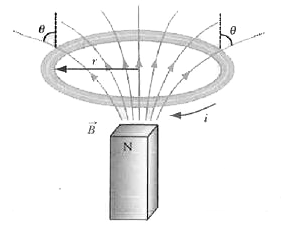
divide the magnetic field into two components and then integrate the force due to each component of the field. We choose the second option.
Calculation : The magnetic field at each point of the ring is having a vertical component of `B cos phi`. This field is uniform and hence the force due to this component of the magnetic field will be zero. The horizontal component of the magnetic field at each element of the rinf will be radially outward. This will produce a force on the element in vertically upward direction as can be seen from Fig.
The magnitude of this force is given by
`dF = idL B sin theta`
The net force acting on the wire is given by
`F = 2pi i r B sin theta`.
We can see that the vertical component of the magnetic field does not contribute to the net force on the wire : however, each element of the wire will be experiencing a force inward. This will tend to contract the wire. The current-carrying loop experiences a force in a nonuniform magnetic field.