A particle of mass m and charge q is moving in a region where uniform, constant electric and mangetic fields →Eand→B are present. →Eand→B are parallel to each other. At time t=0, the velocity →v0 of the particle is perpendicular to →E (Assume that its speed is always <<c, the speed of light in vacuum). Find the velocity →v of the particle at time t. You must express your answer in terms of t,q,m, the vector →v0,→E and →B and their magnitudes →v0,→E and →B.
(1) In this case, we cannot say that that path is circular or a helix with uniform pitch. The motion is rather complicated, here we have to use the Lorentz force.
(2) The forces due to parallel electric and magnetic fields on a charged particle moving perpendicular to the fields will be at right angles to each other (electric foece being along the direction of →E while magnetic force being perpendicular to the plane containing →v and →B). Therefore, the magnetic force will not effect the motion of charged particle in the direction of electric superposition and vice versa. So, the problem is equivalent to superposition of two independent motions as shown.
Calculations : For motion of particle under electric field alone,
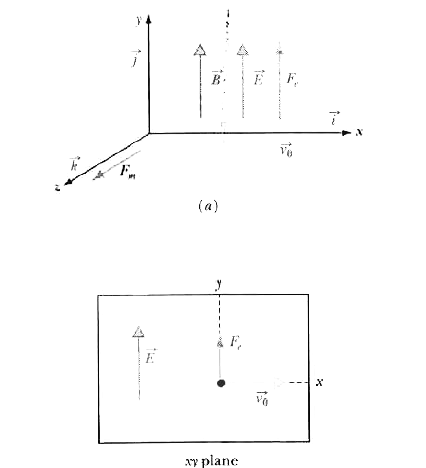
(a) Force on a charged particle in uniform electric and magnetic field. (b) Force on it due to electric field alone. Note that the charge is positive, so the force is in the direction of the electric field. This force is independent of the velocity.
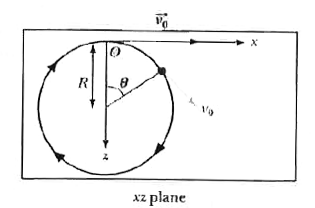
The force due to the magnetic field is always perpendicular to the velocity. So, under its influence, the particle will move in a circular path.
So, the angular position of the particle at time t in the xz plane (or in a plane parallel to xz plane) will be given by
θ=ωt=qBmt.
Hence, in accordance with Fig., we have
vx=v0cosθ=v0cosωt=v0cos(qBm)t,
and vz=v0sin0=v0sinωt=v0sin(qBm)t.
Note that magnetic field does not do any work on the charged particle, so it can change the direction of the velocity v0, but not its magnitude. Also, the angular velocity of its circular motion is independent of its velocity.
So, in the light of Eqs. we have
→v=vxˆi+vyˆj+vzˆk
=v0cos(qBmt)ˆi+(qBmt)ˆj+(qBmt)ˆk.
Since in this case
ˆi=→v0v0,ˆj=→EE=→BB, and ˆk=→v0×→Bv0B
Therefore, we have
→v=v0cos[qBmt][→v0v0]+qEmt→EE]+[v0sin(qBmt)[→v0×→Bv0B].
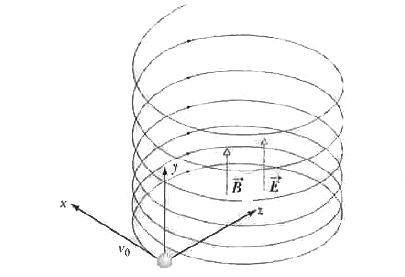
The answer seems to be quite complicated, on analysis of the motion, we see that in the y-direction, the motion is uniformly accelerated. THe motion in xz plane is circular. So, the resultant path is a helix with non-uniform pitch. The path looks like that shown in Fig. As before, the particle repeatedly touches the y axis (if it was projected from the origin) after regular time intervals of T when it has completed one circle. But now the motion along the y axis is accelerated, so the distance between successive points on the y axis where it touches is not the same.
Topper's Solved these Questions
- MAGNETIC FORCEBook:RESNICK AND HALLIDAYChapter:MAGNETIC FORCEExercise:Check point
Explore 6 Videos
- MAGNETIC FORCEBook:RESNICK AND HALLIDAYChapter:MAGNETIC FORCEExercise:Problems
Explore 49 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBook:RESNICK AND HALLIDAYChapter:MAGNETIC FIELDS DUE TO CURRENTSExercise:Practice Question (Integer Type)
Explore 4 Videos
- MOTION ALONG A STRAIGHT LINEBook:RESNICK AND HALLIDAYChapter:MOTION ALONG A STRAIGHT LINEExercise:PRACTICE QUESTIONS ( Integer Type )
Explore 3 Videos
Similar Questions
Knowledge Check
A particle of charge q and mass m starts moving from the origin under the action of an electric field →E=E0ˆi and →B=B0ˆi with a velocity →v=v0ˆj. The speed of the particle will becomes √52v0 after a time
Amv0qE0Bmv02qE0C√3mv02qE0D√5mv02qE0
A particle of mass m and charge q is moving in a region where uniform electric field −−→E and and uniform mag-netic field −−→Bare present. It is given that −−→E∣∣→E∣∣=−−→B∣∣→B∣∣. At time t = 0, velocity of the particle is −−→V0 and −−→V0.−−→E=0. Write the velocity of the particle at time t.
View SolutionAn electric field (vec E) and a magnetic field (vec B)exist in a region . The fields are not perpendicular to each other.
View SolutionIf ∣∣→a+→b∣∣=∣∣→a−→b∣∣, show that the vectors →aand→b are perpendicular to each other.
View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and megnetic field are given by →B=−B0ˆj and →E=→E0ˆk. Find the speed of the particle as a function of its z-coordinate.
View SolutionIf →a+→b+→c=→0, −→|a|=3, ∣∣→b∣∣=5 and |→c|=7.
Find the angle betweeen →a and →b
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionTwo vectors →a and →b are perpendicular to each other if →a.→b=0.
View Solution

