A proton of energy $200 M e V$ enters the magnetic field of $5 T$ . If direction of field is from south to north and motion is upward, the force acting on it will be

Video Solution

Text Solution

Verified by Experts

Because the proton is charged and moving through a magnetic field, a magnetic force ${\to F}_{B}$ can act on it. Because the initial direction of the proton velocity is not along a magnetic field line, ${\to F}_{B}$ is not simply zero.
Magnitude : To find the magnitude of ${\to F}_{B}$ , we can use Eq. 28-3 $(F_{B} - | q | v B sin ϕ)$ provided we first find the proton.s speed v. We can find v from the given kinetic energy because $K = 1 / 2 m v^{2}$ , Solving for v, we obtain
$v = \sqrt{\frac{2 K}{m}} = \sqrt{\frac{(2) (5.3 M e V) (1.60 \times 10^{- 13} J / M e V)}{1.67 \times 10^{- 27} k g}}$
$= 3.2 \times 10^{- 7} m / s$
Equation 28-3 then yields
$F_{B} = | q | v B sin ϕ$
$= (1.60 \times 10^{- 19} C) (3.2 \times 10^{7} m / s) \times (1.2 \times 10^{- 3} T) ({sin 90}^{\circ})$
$= 6.1 \times 10^{- 15} N$ .
This may seem like a small force, but it acts on a particle of small mass, producing a large acceleration, namely,
$a = \frac{F_{B}}{m} = \frac{6.1 \times 10^{- 15} N}{1.67 \times 10^{- 27} k g} = 3.7 \times 10^{12} m / s^{2}$ .
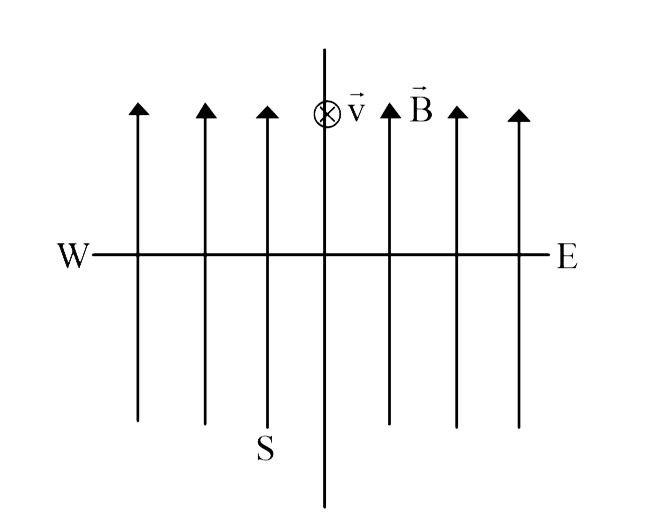
Direction : To find the direction of ${\to F}_{B}$ , we use the fact that ${\to F}_{B}$ has the direction of the cross product $q \to v \times \to B$ . Because the charge q is positiv , ${\to F}_{B}$ must have the same direction as $\to v \times \to B$ , which can determined with the right-hand rule for cross products (as in Fig.) We know that $\to v$ is directed horizontally from south to north and $\to B$ is directed vertically up. The right-hand rule shows us that the deflecting force ${\to F}_{B}$ must be directed horizontally from west to east, as Fig. shows.
If the charge of the particle were negative, the magnetic deflecting force would be directed in the opposite direction - that is, horizontally from east to west. This is predicted automatically by Eq. 28-2 if we substitute a negative value for q.

An downward view of a proton moving from south to north with velocity $\to v$ in a chamber. A magnetic field is directed vertically upward in the chamber, as represented by the array of dots (which resemble the tips of arrows). The proton is deflected toward the east.

Updated on:21/07/2023

A proton with energy of 2 MeV enters a region of a uniform magnetic field of 2.5 T normally. The magnetic force on the proton is (Take mass of proton to be
A $3 \times 10^{- 12} N$
B $3 \times 10^{- 8} N$
C $8 \times 10^{- 12} N$
D $3 \times 10^{- 10} N$
A 5 MeV proton moves vertically downward through a magnetic field of induction $1.5 weber / m^{2}$ pointing horizontally from south to north. The force acting on the proton, mass of proton $= 1.6 \times 10 - 27 k g$ . will be

A $7.44 \times 10^{- 12} N$
B $3.1 \times 10^{- 12} N$
C $5 \times 10^{- 12} N$
D $6 \times 10^{- 12} N$
A proton and an alpha-particle enter a magnetic field in a direction perpendicular to it. If the force acting on the proton is twice that acting on the alpha-particle , the ratio of their velocities is
A $4 : 1$
B $1 : 4$
C $1 : 2$
D $2 : 1$