A resistor, capacitor, switch, and ideal battery are in series. Originally the capacitor is uncharged. The switch is then closed, allowing current of flow
While the current is flowing, the potential difference across the capacitor is
Increasing
Decreasing
Fixed
First increase then decreases
The correct Answer is:A
To solve the problem, we need to analyze the behavior of the capacitor in an RC (resistor-capacitor) circuit when the switch is closed. Let's break down the steps:
Step 1: Understand the Circuit
We have a series circuit consisting of a resistor (R), a capacitor (C), a switch (S), and an ideal battery (V). Initially, the capacitor is uncharged.
Hint: Identify the components in the circuit and their arrangement.
Step 2: Closing the Switch
When the switch is closed, the circuit is completed, allowing current to flow from the battery through the resistor and into the capacitor.
Hint: Remember that closing the switch allows current to start flowing in the circuit.
Step 3: Current Flow and Charging of the Capacitor
As the current flows, the capacitor begins to charge. The charging of the capacitor causes the voltage across it to increase over time. The relationship between the current (I), voltage (V), and resistance (R) can be described by the equation:
VC(t)=V(1−e−t/RC)
Where:
- VC(t) is the voltage across the capacitor at time t,
- V is the voltage of the battery,
- R is the resistance,
- C is the capacitance,
- e is the base of the natural logarithm.
Hint: The voltage across the capacitor increases exponentially as it charges.
Step 4: Potential Difference Across the Capacitor
At the moment the switch is closed, the potential difference across the capacitor starts at 0 volts (since it is initially uncharged) and increases towards the battery voltage V as the capacitor charges.
Hint: The potential difference across the capacitor is initially zero and increases over time.
Step 5: Long-Term Behavior
Eventually, when the capacitor is fully charged, the potential difference across it will equal the voltage of the battery V, and the current will cease to flow.
Hint: Consider what happens to the circuit after a long time has passed.
Conclusion
While the current is flowing, the potential difference across the capacitor is increasing from 0 volts towards the battery voltage V.
---
We have a series circuit consisting of a resistor (R), a capacitor (C), a switch (S), and an ideal battery (V). Initially, the capacitor is uncharged.
When the switch is closed, the circuit is completed, allowing current to flow from the battery through the resistor and into the capacitor.
As the current flows, the capacitor begins to charge. The charging of the capacitor causes the voltage across it to increase over time. The relationship between the current (I), voltage (V), and resistance (R) can be described by the equation:
- VC(t) is the voltage across the capacitor at time t,
- V is the voltage of the battery,
- R is the resistance,
- C is the capacitance,
- e is the base of the natural logarithm.
At the moment the switch is closed, the potential difference across the capacitor starts at 0 volts (since it is initially uncharged) and increases towards the battery voltage V as the capacitor charges.
Eventually, when the capacitor is fully charged, the potential difference across it will equal the voltage of the battery V, and the current will cease to flow.
While the current is flowing, the potential difference across the capacitor is increasing from 0 volts towards the battery voltage V.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Matrix Match)4videos
CIRCUITS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (More than One Correct Choice Type)12videos
CIRCUITS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS6videos
CIRCULAR MOTION
Similar Questions
the final potential difference across the Knowledge Check
- Question 1 - Select One
A resistor, capacitor, switch, and ideal battery are in series. Originally the capacitor is uncharged. The switch is then closed, allowing current of flow
While the current is flowing, the potential difference across the resistor isAIncreasingBDecreasingCFixedDFirst increase then decreases - Question 2 - Select One
In the given circuit, with steady current, the potential difference across the capacitor is
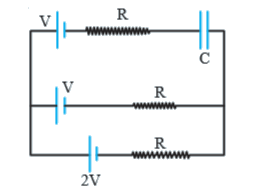AVBV/2C2V/3DNone of these - Question 3 - Select One
If the switch is closed then current will flow.
Afrom A to BBfrom B to AC0Dcannot say unless resistance of galvanometer is given
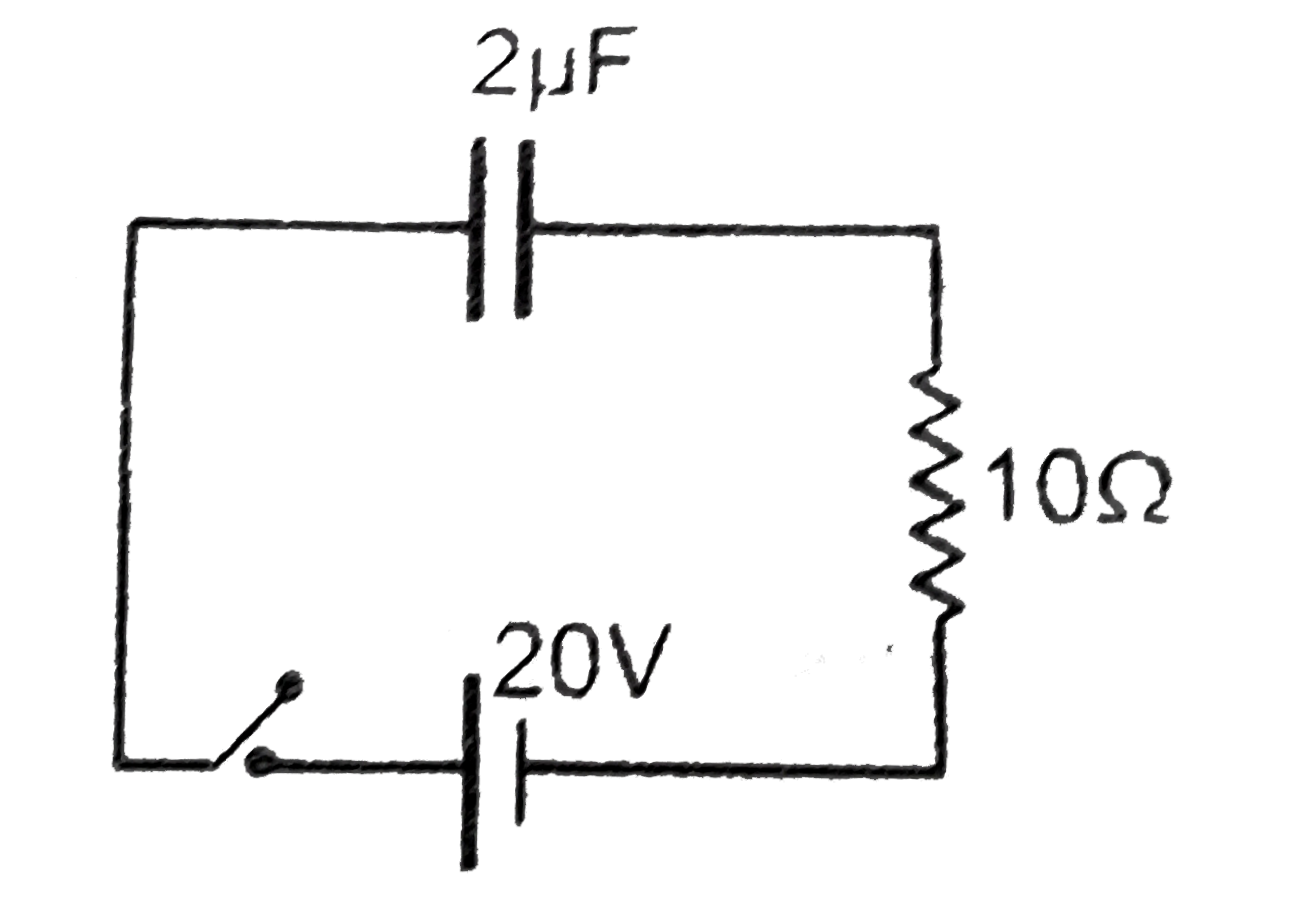
Initially capacitor is uncharged at t=0 switch is closed. Charge on capacitor when current in the circuit is 10% of maximum current :
View SolutionInitially the capacitor was uncharged Current in the capacitor just after switching on will be ?
View SolutionAn ideal capacitor of capacitance 0.2μF is charged to a potential difference of 10V. The charging battery is than disconnected. The capacitor is then connected to an ideal inductor of self inductance 0.5mH. The current at a time when the potential difference across the capacitor is 5V is :
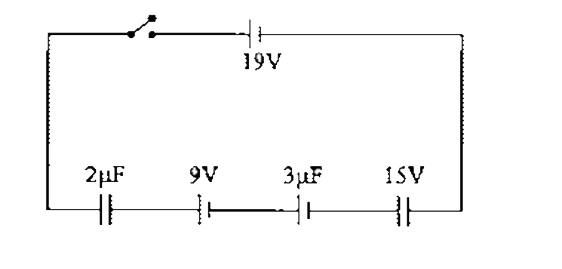
View SolutionThe two capacitors in the circuit shown in figure are initially uncharged and then connected as shown and switch is closed. What is the potential difference across 3μF capacitor?
View Solution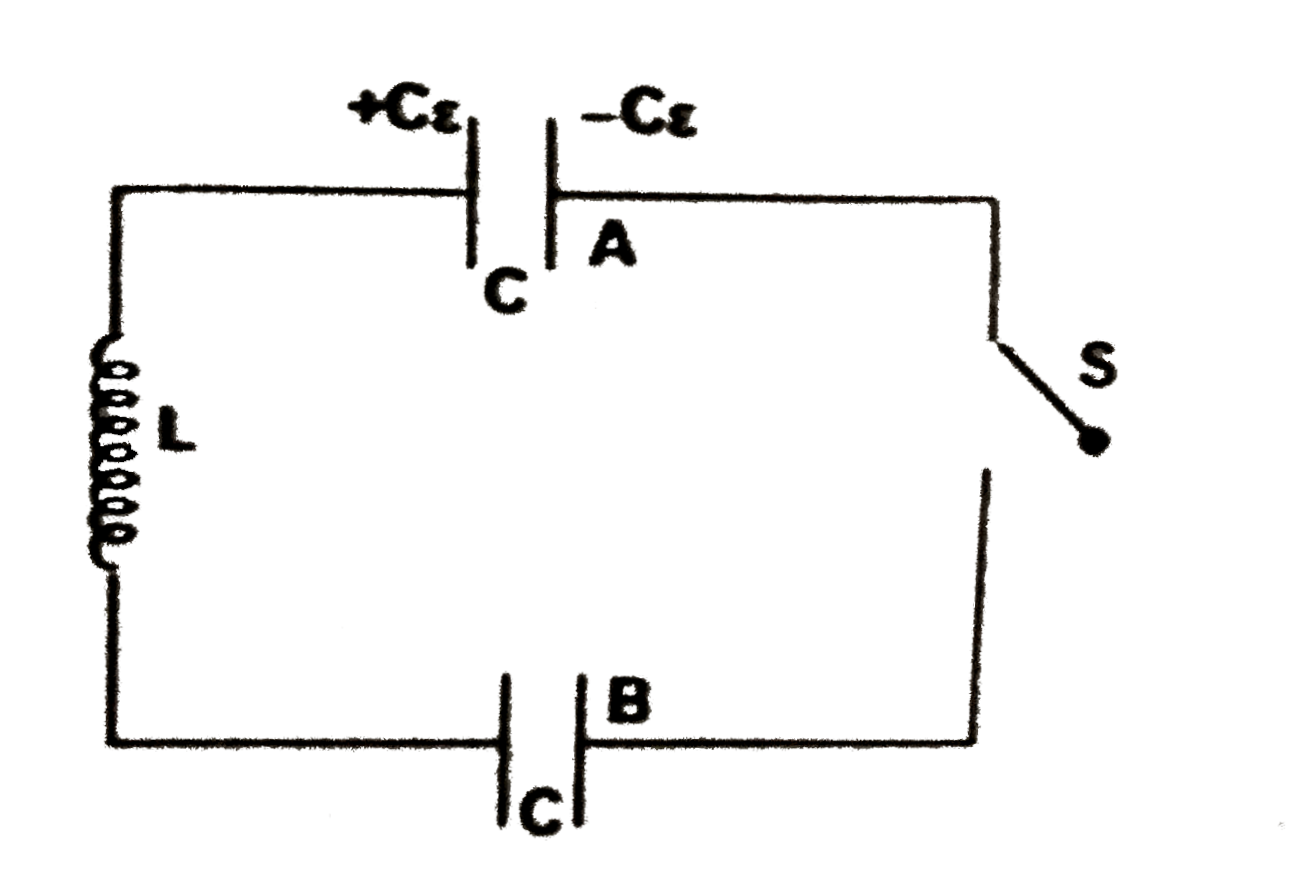
Initially capacitor 'A' is charged to a potential drop ε and capacitor B is uncharged At t=0, switch S is closed, then the maximum current through the inductor isView Solution