Two parallel plate condenser A and B having capacitances of 1μFand5μF are charged separately to the same potential of 100V. Now the positive plate of A is connected to the negative plate of B and the negative plate of A to the positive plate of B.
Energy stored in capacitor is
2×10−2J
3×10−2J
4×10−4J
5×10−5J
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Identify the given values
We have two capacitors:
- Capacitor A: CA=1μF=1×10−6F
- Capacitor B: CB=5μF=5×10−6F
Both capacitors are charged to the same potential:
- Voltage V=100V
Step 2: Calculate the charge on each capacitor
The charge Q stored in a capacitor is given by the formula:
Q=C×V
For capacitor A:
QA=CA×V=(1×10−6F)×(100V)=1×10−4C
For capacitor B:
QB=CB×V=(5×10−6F)×(100V)=5×10−4C
Step 3: Connect the capacitors
When the positive plate of capacitor A is connected to the negative plate of capacitor B and the negative plate of capacitor A is connected to the positive plate of capacitor B, they are effectively connected in parallel.
Step 4: Calculate the net capacitance
The total capacitance Cnet for capacitors in parallel is the sum of their capacitances:
Cnet=CA+CB=1μF+5μF=6μF=6×10−6F
Step 5: Calculate the energy stored in the combined capacitor
The energy U stored in a capacitor is given by the formula:
U=12CV2
Using the net capacitance and the voltage:
U=12×Cnet×V2=12×(6×10−6F)×(100V)2
Calculating this gives:
U=12×(6×10−6)×(10000)=3×10−2J
Final Answer
The energy stored in the capacitor is:
U=3×10−2J
---
We have two capacitors:
- Capacitor A: CA=1μF=1×10−6F
- Capacitor B: CB=5μF=5×10−6F
Both capacitors are charged to the same potential:
- Voltage V=100V
The charge Q stored in a capacitor is given by the formula:
Q=C×V
For capacitor A:
QA=CA×V=(1×10−6F)×(100V)=1×10−4C
For capacitor B:
QB=CB×V=(5×10−6F)×(100V)=5×10−4C
When the positive plate of capacitor A is connected to the negative plate of capacitor B and the negative plate of capacitor A is connected to the positive plate of capacitor B, they are effectively connected in parallel.
The total capacitance Cnet for capacitors in parallel is the sum of their capacitances:
Cnet=CA+CB=1μF+5μF=6μF=6×10−6F
The energy U stored in a capacitor is given by the formula:
U=12CV2
Using the net capacitance and the voltage:
U=12×Cnet×V2=12×(6×10−6F)×(100V)2
Calculating this gives:
U=12×(6×10−6)×(10000)=3×10−2J
The energy stored in the capacitor is:
U=3×10−2J
Topper's Solved these Questions
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION MATRIX MATCH
8 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)
3 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
12 Videos
- ALL ABOUT ATOMS BOOK - RESNICK AND HALLIDAYCHAPTER - ALL ABOUT ATOMS EXERCISE - CHECKPOINT
1 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
Similar Questions
Two parallel plates capacitors A and B having capacitance of 1μFand5μF are charged separately to the same potential of 100 V. Now, the positive plate of A is connected to the negative plate of B and the negative plate of A to the positive plate of B. Find the final charges on each capacitors.
View SolutionA capacitor A of capacitance 4μF is charged to 30V and another capacitor B of capacirtance μF is charged to 15V. Now, the opositive plate of A is connected to the negative plate of B and negative plate of A to the positive plate of B. find the final charge of each capacitor and loss of electrostatic energy in the process.
View Solution
Knowledge Check
Two parallel plate condenser A and B having capacitances of 1μFand5μF are charged separately to the same potential of 100V. Now the positive plate of A is connected to the negative plate of B and the negative plate of A to the positive plate of B.
Final energy stored in capacitor isA1.67JB6.71JC1.2JD1.33JTwo parallel plate condenser A and B having capacitances of 1μFand5μF are charged separately to the same potential of 100V. Now the positive plate of A is connected to the negative plate of B and the negative plate of A to the positive plate of B.
Common potential isA2005VB2003VC2004VD2007VTwo capacitors of capacitance 2μF and 4μF respectively are charged to a potential of 12 V. they are now connected to each other, with the positive plate of each joined to the negative plate of the other. The potential difference across each capacitor will be
A2 VB3VC4VD6V
Three capcaitors of capacities 1μF,2μF and 3μF are charged by 10V,20V and 30V respectively. Now positive plates of first two capacitors are connected with the negative plate of third capacitor on one side and negative plates of first wo capacitors are connectes with positive of third capacitor on the other side. Find
a. common potential V
b. final charges on different capacitors.
View SolutionTwo capacitors of capacitances 3μF and 6μF are charged to a potential of 12V each. They are now connected to each other, with the positive plate of each joined to the negative plate of the other. The potential difference across each will be
View SolutionTwo capacitors A and B of capacitances 2μF and 5μF are connected to two battery as shown in figure The potential difference in volt between the plate of A is
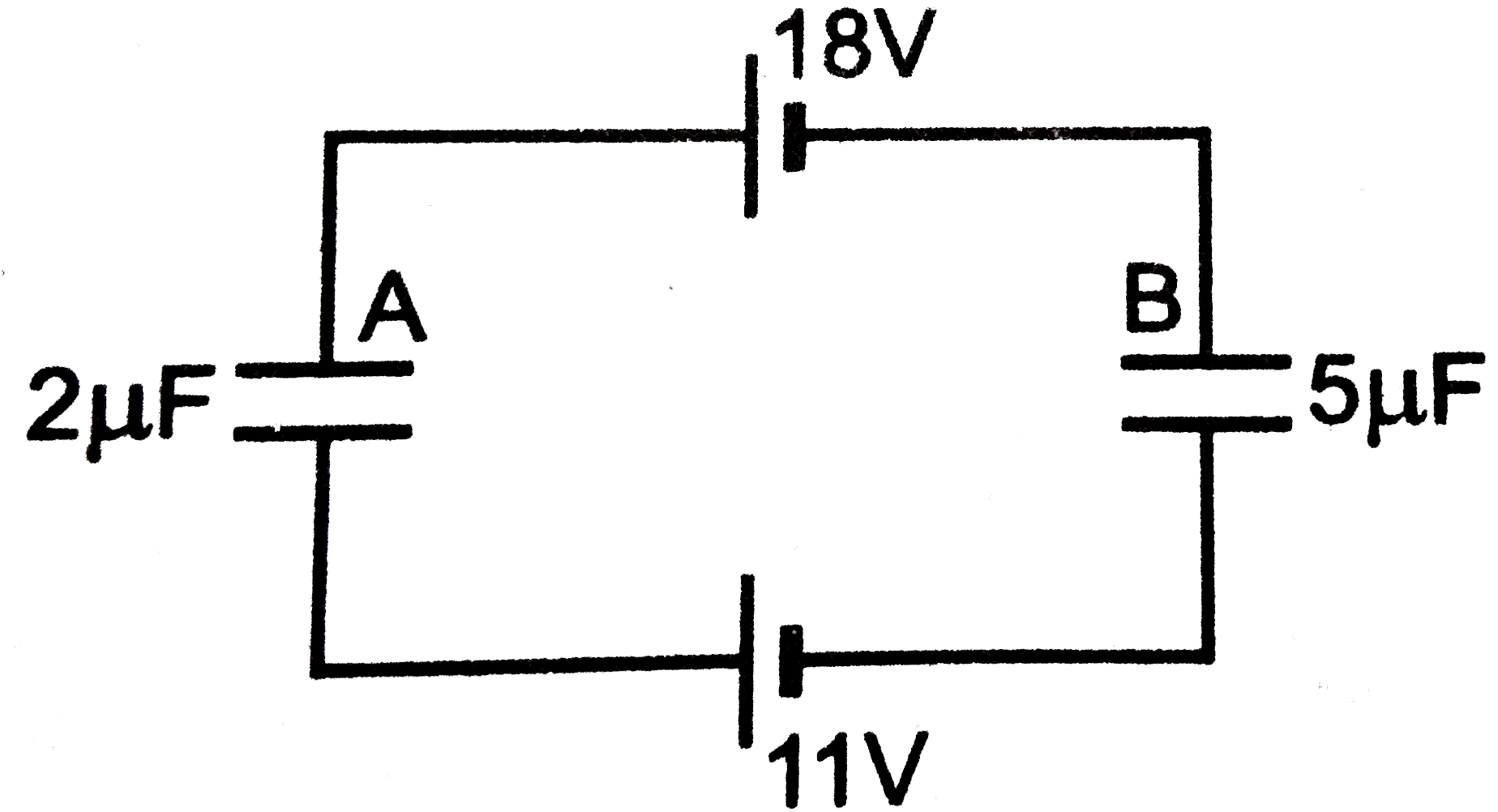
View SolutionTwo capacitors of capacitance 2μFand5μF are charged to a potential difference 100V and 50 V respectively and connected such that the positive plate of one capacitor is connected to the negative plate of the other capacitor after the switch is closed, the initial current in the circuit is 50 mA. the total resistance of the connecting wires is (in Ohm):
View SolutionTwo identical capacitors are joined in parallel, charged to a potential V and then separated and then connected in series i.e. the positive plate of one is connected to negative of the other
View Solution
