Assume that a stationary electron is a point of charge . What is the energy density u of its electric field at radial distances (a) r=1.00 mm, (b) r=1.00 μm ( c) r=1.00 nm (d) r=1.00 pm, and (e ) r=1.00 fm (f) What is the u in the limit as r→0?
To solve the question regarding the energy density u of the electric field of a stationary electron at various radial distances, we will follow these steps:
1. Understand the Formula for Energy Density:
The energy density u of an electric field is given by the formula:
u=12ϵ0E2
where ϵ0 is the permittivity of free space and E is the electric field strength.
2. Electric Field of a Point Charge:
The electric field E due to a point charge q at a distance r is given by:
E=k⋅|q|r2
where k is Coulomb's constant, k=14πϵ0.
3. Substituting Electric Field into Energy Density:
Substitute E into the energy density formula:
u=12ϵ0(k⋅|q|r2)2
Simplifying this gives:
u=12ϵ0⋅k2⋅q2r4
Since k=14πϵ0, substituting this in gives:
u=12ϵ0⋅(1/(4πϵ0))2⋅q2r4
Simplifying further, we find:
u=q232π2ϵ0r4
4. Using the Charge of the Electron:
The charge of an electron q=1.6×10−19C and the permittivity of free space ϵ0=8.85×10−12F/m.
5. Calculating Energy Density for Different Distances:
Now, we will calculate u for the given distances:
- (a) r=1.00mm=1.00×10−3m:
u=(1.6×10−19)232π2(8.85×10−12)(1.00×10−3)4≈9.16×10−18J/m3
- (b) r=1.00μm=1.00×10−6m:
u≈9.16×10−12J/m3
- (c) r=1.00nm=1.00×10−9m:
u≈9.16×106J/m3
- (d) r=1.00pm=1.00×10−12m:
u≈9.16×1018J/m3
- (e) r=1.00fm=1.00×10−15m:
u≈9.16×1030J/m3
6. Limit as r→0:
As r approaches 0, the energy density u tends to infinity:
limr→0u=∞
Summary of Results:
- u at r=1.00mm: 9.16×10−18J/m3
- u at r=1.00μm: 9.16×10−12J/m3
- u at r=1.00nm: 9.16×106J/m3
- u at r=1.00pm: 9.16×1018J/m3
- u at r=1.00fm: 9.16×1030J/m3
- u as r→0: ∞
The energy density u of an electric field is given by the formula:
u=12ϵ0E2
where ϵ0 is the permittivity of free space and E is the electric field strength.
The electric field E due to a point charge q at a distance r is given by:
E=k⋅|q|r2
where k is Coulomb's constant, k=14πϵ0.
Substitute E into the energy density formula:
u=12ϵ0(k⋅|q|r2)2
Simplifying this gives:
u=12ϵ0⋅k2⋅q2r4
Since k=14πϵ0, substituting this in gives:
u=12ϵ0⋅(1/(4πϵ0))2⋅q2r4
Simplifying further, we find:
u=q232π2ϵ0r4
The charge of an electron q=1.6×10−19C and the permittivity of free space ϵ0=8.85×10−12F/m.
Now, we will calculate u for the given distances:
u=(1.6×10−19)232π2(8.85×10−12)(1.00×10−3)4≈9.16×10−18J/m3
u≈9.16×10−12J/m3
u≈9.16×106J/m3
u≈9.16×1018J/m3
u≈9.16×1030J/m3
As r approaches 0, the energy density u tends to infinity:
limr→0u=∞
- u at r=1.00mm: 9.16×10−18J/m3
- u at r=1.00μm: 9.16×10−12J/m3
- u at r=1.00nm: 9.16×106J/m3
- u at r=1.00pm: 9.16×1018J/m3
- u at r=1.00fm: 9.16×1030J/m3
- u as r→0: ∞
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)23videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)12videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - CHECKPOINTS4videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - ALL ABOUT ATOMS EXERCISE - CHECKPOINT1videos
ALL ABOUT ATOMS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
Similar Questions
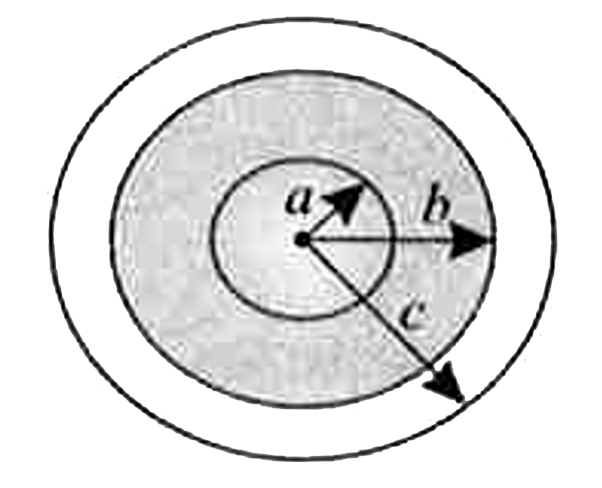
In figure , a solid sphere of radius a = 2.00cm is concentric with a spherical conduction shell of inner radius b =2.00 a and outer radius c=2.40 a. the sphere has a net uniform charge q1=+5.00C. The shell has a net charge q2=−q1. Distance (a) r=0 (b) r= a/2.00 (c) r=a (d) r = 1.50 a (e) r= 2.30a and (f) r= 3.50 a ? what si the net charge on the (g) inner and (h) outer surface of the shell ?
 View Solution
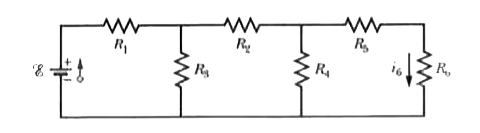
View SolutionIn Fig. 27-43, the current in resistance 6 is i6=2.80A the resistances are R1=R2=R3=2.00Ω,R4=16.0Ω,R5=8.00ΩandR6=4.00Ω. Wat is the emf of the ideal battery?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
A2qd4πε0(d2+a2)3/2ˆkBqd4πε0(d2+a2)3/2ˆkC−2qd4πε0(d2+a2)3/2ˆkD−qd4πε0(d2+a2)3/2ˆk - Question 2 - Select One
Two switch in the figurte is open for t<0 and is the thrown closed at time t=0. Assume R=4.00ω,L=1.00H, and ε=10.0V.

The current in the inductor as functions of timeA(0.5A)[1−e−20t/s]B(0.5A)[1−e−10/s]C(2.5A)[1−e−10/s]D(0.5A)[1−e−15/s] - Question 3 - Select One
Two switch in the figurte is open for t<0 and is the thrown closed at time t=0. Assume R=4.00ω,L=1.00H, and ε=10.0V.

The current in the switch as functions of time t.A2.5A−(0.25A)e−10t/sB1.5A−(0.5A)e−10t/sC2.5A−(0.5A)e−10t/sD1.5A−(0.25A)e−10t/s
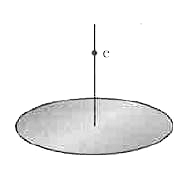
In Fig. an electron (e) is to be released from rest on the central axis of a uniformly charged disk of radius R. The surface charge density on the disk is +5.00μC/m2. What is the magnitude of the electron's initial acceleration if it is released at a distance (a) R, (b) R/100, and (c ) R/1000 from the center of the disk ? (d) Why does the acceleration magnitude increase only slightly as the release point is moved closer to the disk ?
 View Solution
View SolutionWhat is the probability that an electron in the ground state of the hydrogen atom will be found between two spherical shells whose radii are r and r+Δr, (a) if r = 0.500a and Δr = 0.010a and (b) if r = 1.00a and Δr = 0.01a, where a is the Bohr radius? (Hint: Δr is small enough to permit the radial probability density to be taken to be constant between r and r+Δr.)
View Solutionshows, in cross section, a plastic, spherical shell with uniform charge Q=−16e and radius R=10cm. A particle with charge q=+5e is at the center. What is the electric field (magnitude and direction) at (a) point P1 at radial distance r1=6.00cm and (b) point P2 at radial distance r2=12.0cm ?
View SolutionHow many times are the hour hand and the minute hand of a clock at right angles during their motion from 1.00 p.m. to 10.00 p.m.? (a) 9 (b) 10 (c) 18 (d) 20
View SolutionWhat is the fraction of the solute in a 1.00 m aqueous solution ?
View Solution
