A firefighter who weighs 689 N slides down a vertical pole with an acceleration of 2.00 m/s2, directed downward. What are the (a) magnitude and (b) direction (up or down) of the vertical force on the firefighter from the pole and the ( c ) magnitude and (d) direction of the vertical force on the pole from the firefighter ?
To solve the problem step by step, we will analyze the forces acting on the firefighter and apply Newton's second law of motion.
Step 1: Identify the forces acting on the firefighter
The forces acting on the firefighter are:
- The weight of the firefighter (W) acting downward, which is given as 689 N.
- The frictional force (F_k) exerted by the pole on the firefighter, which acts upward.
Step 2: Write the equation of motion
According to Newton's second law, the net force (F_net) acting on the firefighter can be expressed as:
Fnet=m⋅a
where m is the mass of the firefighter and a is the acceleration (2.00 m/s² downward).
Step 3: Calculate the mass of the firefighter
The weight of the firefighter is given by:
W=m⋅g
where g is the acceleration due to gravity (approximately 9.8 m/s²). We can rearrange this to find the mass:
m=Wg=689N9.8m/s2≈70.3kg
Step 4: Set up the equation for net force
The net force acting on the firefighter can be expressed as:
Fnet=W−Fk
Substituting the values we have:
m⋅a=W−Fk
70.3⋅2.00=689−Fk
Step 5: Solve for the frictional force (F_k)
Calculating the left side:
140.6=689−Fk
Rearranging to solve for Fk:
Fk=689−140.6=548.4N
Step 6: Determine the direction of the forces
(a) The magnitude of the vertical force on the firefighter from the pole is 548.4 N.
(b) The direction of this force is upward, as it is the frictional force opposing the downward motion.
Step 7: Analyze the force on the pole from the firefighter
According to Newton's third law, the force exerted by the firefighter on the pole will be equal in magnitude and opposite in direction to the force exerted by the pole on the firefighter.
(c) The magnitude of the vertical force on the pole from the firefighter is also 548.4 N.
(d) The direction of this force is downward, as it acts in the opposite direction to the force exerted by the pole on the firefighter.
Summary of Answers:
(a) Magnitude of the vertical force on the firefighter from the pole: 548.4 N
(b) Direction of the vertical force on the firefighter from the pole: Upward
(c) Magnitude of the vertical force on the pole from the firefighter: 548.4 N
(d) Direction of the vertical force on the pole from the firefighter: Downward
The forces acting on the firefighter are:
- The weight of the firefighter (W) acting downward, which is given as 689 N.
- The frictional force (F_k) exerted by the pole on the firefighter, which acts upward.
According to Newton's second law, the net force (F_net) acting on the firefighter can be expressed as:
Fnet=m⋅a
where m is the mass of the firefighter and a is the acceleration (2.00 m/s² downward).
The weight of the firefighter is given by:
W=m⋅g
where g is the acceleration due to gravity (approximately 9.8 m/s²). We can rearrange this to find the mass:
m=Wg=689N9.8m/s2≈70.3kg
The net force acting on the firefighter can be expressed as:
Fnet=W−Fk
Substituting the values we have:
m⋅a=W−Fk
70.3⋅2.00=689−Fk
Calculating the left side:
140.6=689−Fk
Rearranging to solve for Fk:
Fk=689−140.6=548.4N
(a) The magnitude of the vertical force on the firefighter from the pole is 548.4 N.
(b) The direction of this force is upward, as it is the frictional force opposing the downward motion.
According to Newton's third law, the force exerted by the firefighter on the pole will be equal in magnitude and opposite in direction to the force exerted by the pole on the firefighter.
(d) The direction of this force is downward, as it acts in the opposite direction to the force exerted by the pole on the firefighter.
(a) Magnitude of the vertical force on the firefighter from the pole: 548.4 N
(b) Direction of the vertical force on the firefighter from the pole: Upward
(c) Magnitude of the vertical force on the pole from the firefighter: 548.4 N
(d) Direction of the vertical force on the pole from the firefighter: Downward
Topper's Solved these Questions
- FORCE AND MOTION - I Book:RESNICK AND HALLIDAYChapter:FORCE AND MOTION - I Exercise:PRACTICE QUESTIONS (Single Correct Choice Type)
Explore 36 Videos
- FORCE AND MOTION - I Book:RESNICK AND HALLIDAYChapter:FORCE AND MOTION - I Exercise:PRACTICE QUESTIONS (More than One Correct Choice Type)
Explore 5 Videos
- FORCE AND MOTION - I Book:RESNICK AND HALLIDAYChapter:FORCE AND MOTION - I Exercise:CHECKPOINT
Explore 5 Videos
- FLUIDSBook:RESNICK AND HALLIDAYChapter:FLUIDSExercise:PRACTICE QUESTIONS (Integer Type )
Explore 5 Videos
- FORCE AND MOTION-IIBook:RESNICK AND HALLIDAYChapter:FORCE AND MOTION-IIExercise:PRACTICE QUESTIONS (Integer Type)
Explore 1 Video
Similar Questions
Figure shows a 0.300 kg baseball just before and just after it collides with a bat. Just before, the ball has velocity →v1 of magnitude 12.0 m/s and angle θ1=35.0∘ Just after, it is traveling directly upward with velocity →v2 of magnitude 10.0 m/s The duration of the collision is 2.00 ms. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the impulse on the ball from the bat? What are the (c) magnitude and (d) direction of the average force on the ball from the bat?
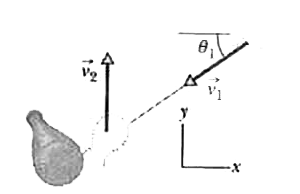
View SolutionMention the magnitude and direction of the net force each case. (Take g=10 m s−2)
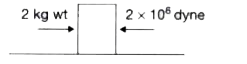
View Solution
Knowledge Check
A 20 kg monkey slides down a vertical rope with a constant acceleration of 7ms−2. If g=10m/s−2, what is the tension in the rope ?
A140 NB100 NC60 ND30 NWhat is the magnitude and direction of the electric force on a −1.2μC charge at a point where the electric field is 2500 N/C and is directed along the +y axis.
A0.15 N, -y directionB0.0030 N, -y directionC0.15 N, +y directionD0.0030 N, +y direction
Mention the magnitude and direction of the net force each case. (Take g=10 m s−2)

View SolutionA helicopter of mass 2000 kg rises with a vertical acceleration of 15ms−2. The total mass of the crew and passengers is 500 kg. Give the magnitude and direction of the (g=10ms−2)
(a) Force on the floor of the helicopter by the crew and passengers.
(b) action of the rotor of the helicopter on the surrounding air.
(c ) force on the helicopter dur to the surrounding air.
View SolutionA helicopter of mass 2000 kg rises with a vertical acceleration of 15ms−2. The total mass of the crew and passengers is 500 kg. Give the magnitude and direction of the (g=10ms−2)
(a) Force on the floor of the helicopter by the crew and passengers.
(b) action of the rotor of the helicopter on the surrounding air.
(c ) force on the helicopter dur to the surrounding air.
View SolutionA helicopter of mass 2000 kg rises with a vertical acceleration of 15ms−2. The total mass of the crew and passengers is 500 kg. Give the magnitude and direction of the (g=10ms−2)
(a) Force on the floor of the helicopter by the crew and passengers.
(b) action of the rotor of the helicopter on the surrounding air.
(c ) force on the helicopter dur to the surrounding air.
View SolutionA helicopter of mass 2000 kg rises with a vertical acceleration of 15ms−2. The total mass of the crew and passengers is 500 kg. Give the magnitude and direction of the (g=10ms−2)
(a) Force on the floor of the helicopter by the crew and passengers.
(b) action of the rotor of the helicopter on the surrounding air.
(c ) force on the helicopter dur to the surrounding air.
View Solution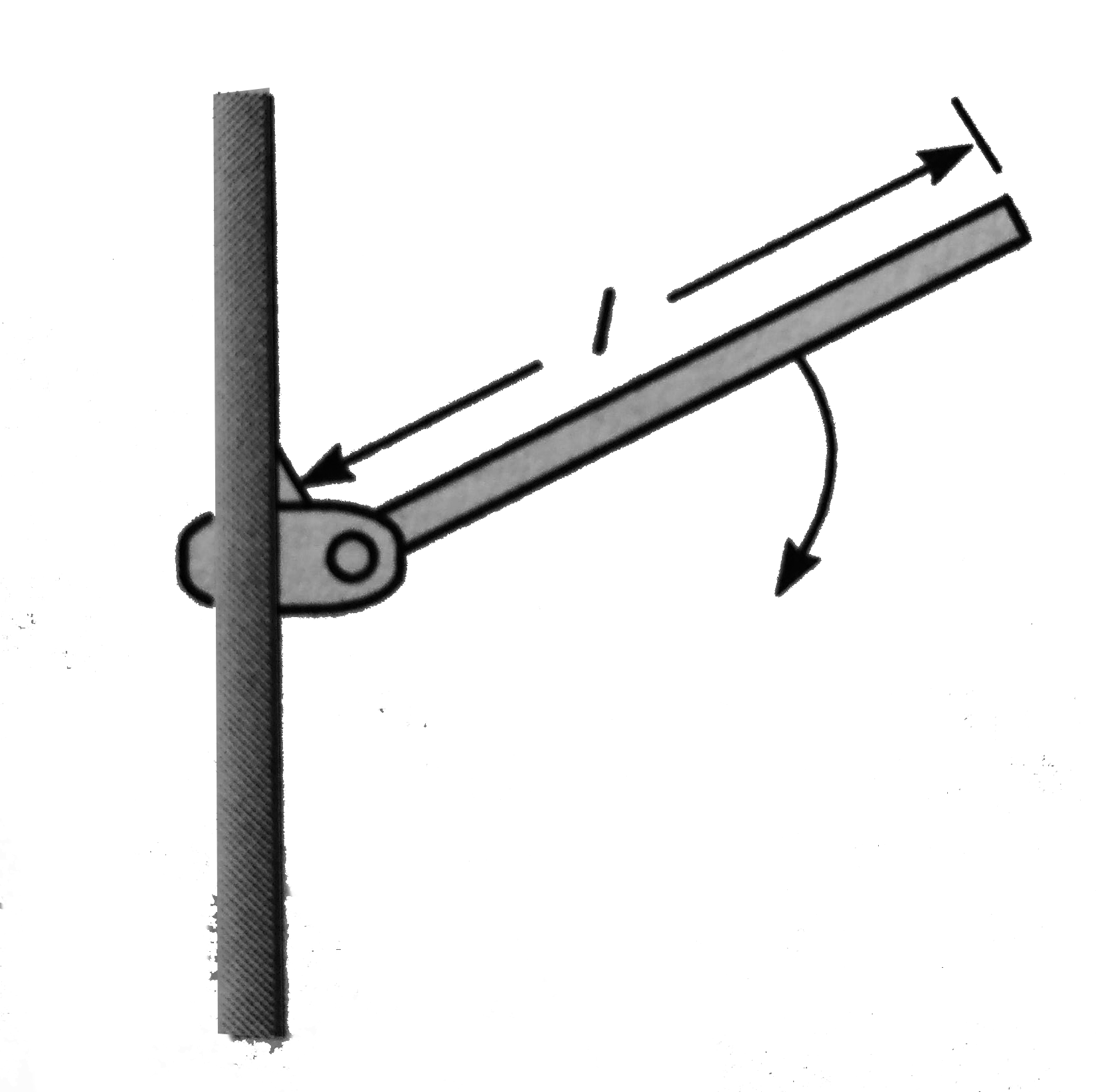
A thin plank of mass M and length l is pivoted at one end. The plank is releaed at 60∘ from the vertical. What is the magnitude and direction of the force on the pivot when the plank is horizontal?
View Solution