A bead of mass 2.5×10−4 kg is suspended from a cord. A steady horizontal breeze pushes the bead so that the cord makes a constant angle of 40∘ with the vertical. Find (a) the tension in the cord and (b) the push magnitude.
To solve the problem step by step, we will analyze the forces acting on the bead and use trigonometric relationships to find the tension in the cord and the push magnitude.
Step 1: Identify the forces acting on the bead
The forces acting on the bead are:
- The weight of the bead (mg) acting vertically downward.
- The tension (T) in the cord acting along the cord.
- The horizontal push (F) acting horizontally.
Step 2: Draw the Free Body Diagram (FBD)
In the FBD, we can see:
- The weight (mg) acting downward.
- The tension (T) making an angle of 40 degrees with the vertical.
- The horizontal push (F) acting horizontally.
Step 3: Resolve the tension into components
The tension T can be resolved into two components:
- The vertical component: Tcos(40∘)
- The horizontal component: Tsin(40∘)
Step 4: Set up the equations
From the FBD, we can set up the following equations based on the equilibrium of forces:
1. In the vertical direction:
Tcos(40∘)=mg
2. In the horizontal direction:
Tsin(40∘)=F
Step 5: Calculate the weight of the bead
Given:
- Mass of the bead, m=2.5×10−4 kg
- Acceleration due to gravity, g=10m/s2
Calculate the weight:
mg=2.5×10−4kg×10m/s2=2.5×10−3N
Step 6: Substitute into the vertical equation to find T
Substituting mg into the vertical force equation:
Tcos(40∘)=2.5×10−3N
Now, we need the value of cos(40∘):
cos(40∘)≈0.766
Now, substituting this value:
T⋅0.766=2.5×10−3
T=2.5×10−30.766≈3.26×10−3N≈3.26mN
Step 7: Calculate the push magnitude F
Using the horizontal force equation:
F=Tsin(40∘)
Now, we need the value of sin(40∘):
sin(40∘)≈0.643
Substituting the value of T:
F=(3.26×10−3)⋅0.643≈2.09×10−3N≈2.09mN
Final Answers:
(a) The tension in the cord, T≈3.26mN
(b) The push magnitude, F≈2.09mN
---
The forces acting on the bead are:
- The weight of the bead (mg) acting vertically downward.
- The tension (T) in the cord acting along the cord.
- The horizontal push (F) acting horizontally.
In the FBD, we can see:
- The weight (mg) acting downward.
- The tension (T) making an angle of 40 degrees with the vertical.
- The horizontal push (F) acting horizontally.
The tension T can be resolved into two components:
- The vertical component: Tcos(40∘)
- The horizontal component: Tsin(40∘)
From the FBD, we can set up the following equations based on the equilibrium of forces:
1. In the vertical direction:
Tcos(40∘)=mg
2. In the horizontal direction:
Tsin(40∘)=F
Given:
- Mass of the bead, m=2.5×10−4 kg
- Acceleration due to gravity, g=10m/s2
mg=2.5×10−4kg×10m/s2=2.5×10−3N
Substituting mg into the vertical force equation:
Tcos(40∘)=2.5×10−3N
cos(40∘)≈0.766
T⋅0.766=2.5×10−3
T=2.5×10−30.766≈3.26×10−3N≈3.26mN
Using the horizontal force equation:
F=Tsin(40∘)
sin(40∘)≈0.643
F=(3.26×10−3)⋅0.643≈2.09×10−3N≈2.09mN
(a) The tension in the cord, T≈3.26mN
Topper's Solved these Questions
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
36 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
5 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - CHECKPOINT
5 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )
5 Videos
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
1 Videos
Similar Questions
(a) How many revolutions per minute must the apparatus shown in figure make about a vertical axis so that the cord makes an angle of 45∘ with the vertical ?

(b)What is the tension in the cord then? Given, l=√2m,a=20cm and m=5.0kg?
View SolutionA weight of mass m is suspended from a cord so that one section of it makes an angle alph1 with the horizontal and the other - an angle α2 (Fig.). Find the tension of these sections of the cord.
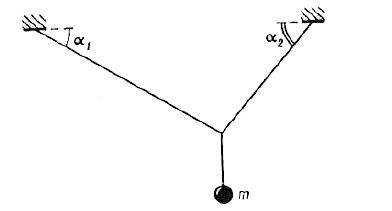
View Solution
Knowledge Check
A mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
A20 kg-wtB10 kg-wtC10√3 kg-wtD20√3 kg-wtA mass of 10 kg is suspended from a spring balance, it is pulled aside by a horizontal string so that it makes an angle 60∘ with the vertical. The new reading of the balance is:
A10√3 kg wtB20√3 kg wtC20 kg wtD10 kg wtA heavy particle of mass 1kg suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle 30∘ with the vertical. The magnitude of the force F equals
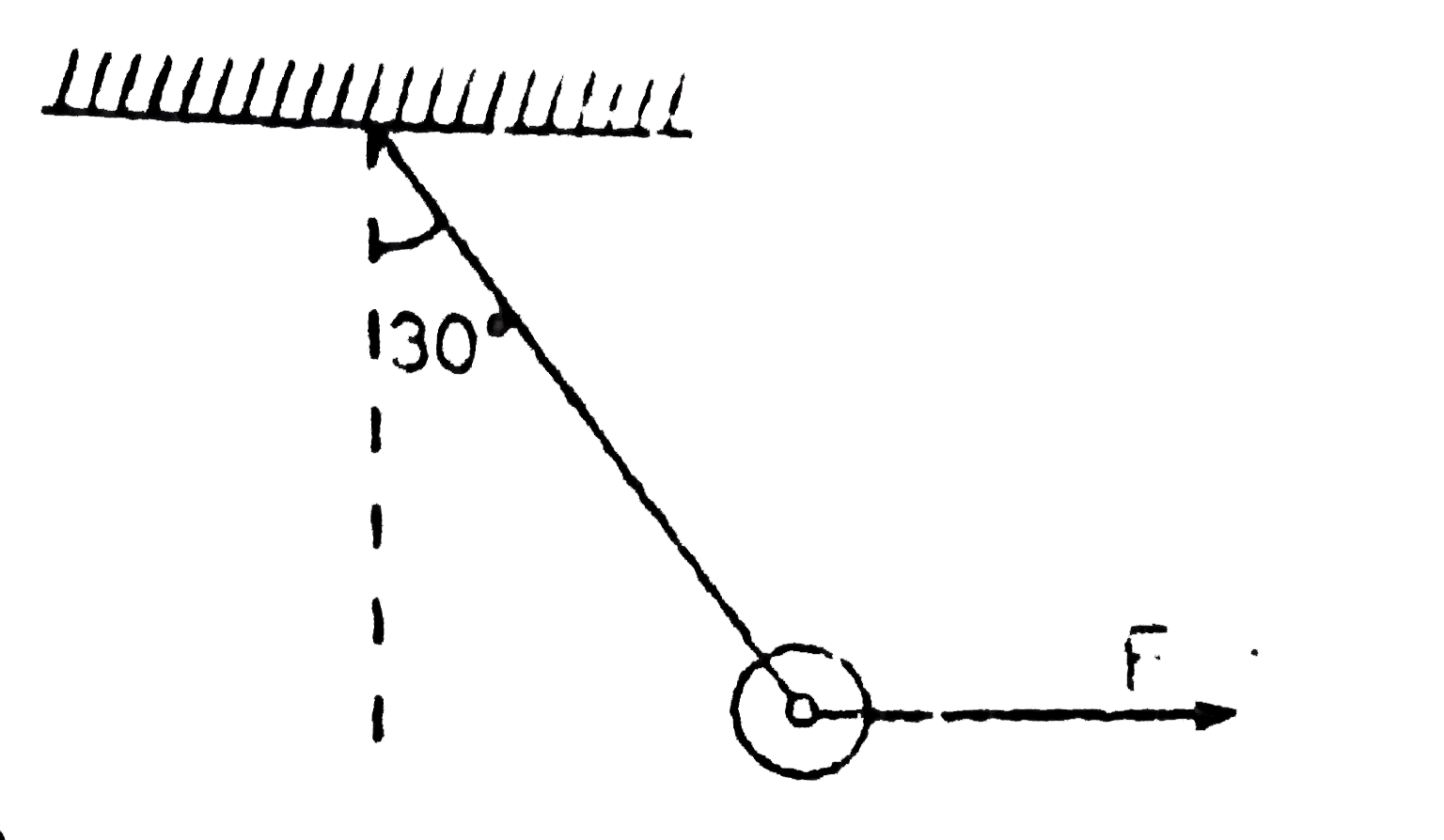 .A10NB10√3NC5ND10√3N
.A10NB10√3NC5ND10√3N
The bob of a 0.2 m pendulum describs an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is g/n. Find value of n.
View SolutionThe bob of a 0.2 m pendulum describes an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is
View SolutionA block of mass m=15g is suspended in an elevator with the help of three identical light elastic cords (spring constant k=100N/m each) attached vertically. One of them cord 1 is tied to the ceilling of the elevator and the other two cords 2 and 3 are tied to the elevator floor as shown in the figure. When the elevator is stationary the tension force is each of the lower cords is T=7.5N. Take g=10m/s2. Now the elevator starts moving with given four accelerations shown in column I. Column II given the displacement of the block with respect to elevator when its is accelerating. Column III gives tension in the cords when elevator is accelerating.
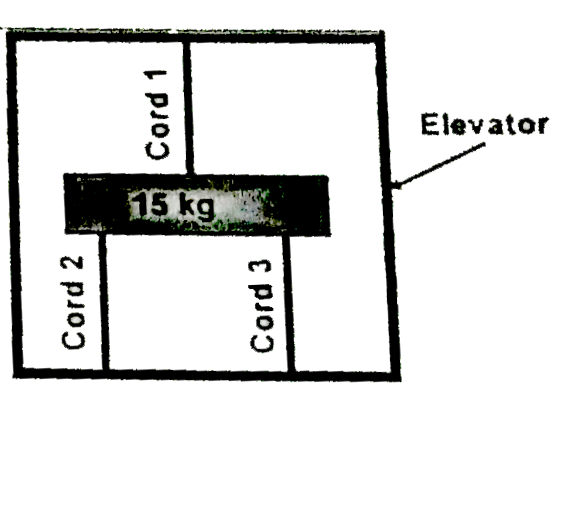

Tension in cord -2
View SolutionA block of mass m=15g is suspended in an elevator with the help of three identical light elastic cords (spring constant k=100N/m each) attached vertically. One of them cord 1 is tied to the ceilling of the elevator and the other two cords 2 and 3 are tied to the elevator floor as shown in the figure. When the elevator is stationary the tension force is each of the lower cords is T=7.5N. Take g=10m/s2. Now the elevator starts moving with given four accelerations shown in column I. Column II given the displacement of the block with respect to elevator when its is accelerating. Column III gives tension in the cords when elevator is accelerating.
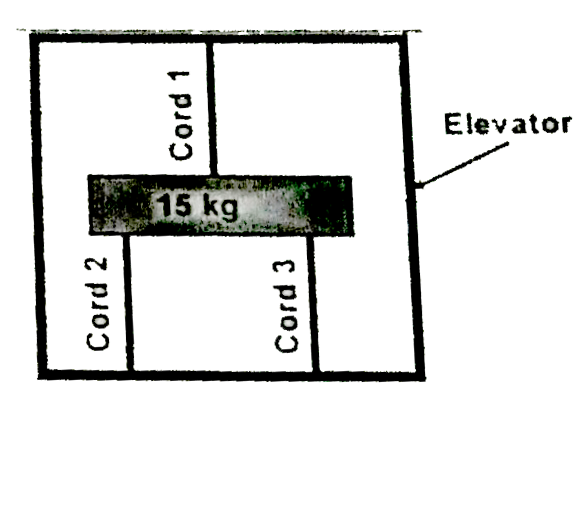
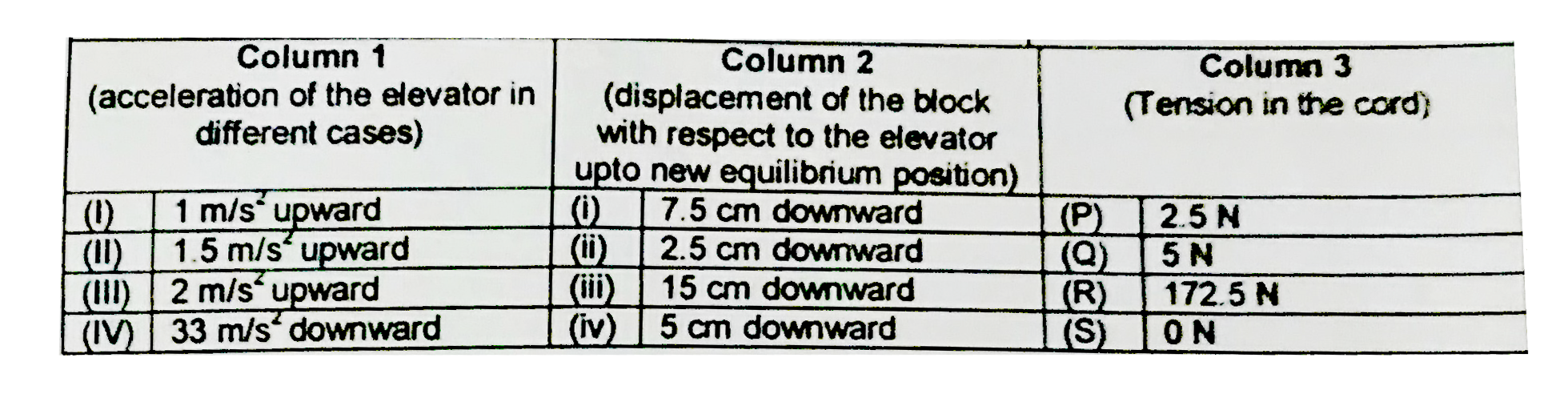
Tension in cord -1
View SolutionA block of mass m=15g is suspended in an elevator with the help of three identical light elastic cords (spring constant k=100N/m each) attached vertically. One of them cord 1 is tied to the ceilling of the elevator and the other two cords 2 and 3 are tied to the elevator floor as shown in the figure. When the elevator is stationary the tension force is each of the lower cords is T=7.5N. Take g=10m/s2. Now the elevator starts moving with given four accelerations shown in column I. Column II given the displacement of the block with respect to elevator when its is accelerating. Column III gives tension in the cords when elevator is accelerating.


Tension in cord -3
View Solution
