Consider two intersecting (non-perpendicular lines L1=0andL2=0 and a point P1. Image of P1 and L1=0 is P2, image of P2 in L2=0 is P3 , image of P3 in L1 =0 is P4 and so on. Which of the following statements are incorrect ?
−−−→P3P5=−−−→P4P6
−−−→P1P4=−−−→P2P3
Pi are concylic
P5 is P14
The correct Answer is:D
Step by step video, text & image solution for Consider two intersecting (non-perpendicular lines L_(1)=0 and L_(2)=0 and a point P_(1). Image of P_(1) and L_(1)=0 is P_(2), image of P_(2) in L_(2)=0 is P_(3) , image of P_(3) in L_(1) =0 is P_(4) and so on. Which of the following statements are incorrect ? by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STRAIGHT LINESBook:OBJECTIVE RD SHARMAChapter:STRAIGHT LINESExercise:Chapter Test
Explore 34 Videos
- STRAIGHT LINESBook:OBJECTIVE RD SHARMAChapter:STRAIGHT LINESExercise:SECTION - II (ASSERTION - REASON TYPE MCQs
Explore 1 Video
- SETSBook:OBJECTIVE RD SHARMAChapter:SETSExercise:Chapter Test
Explore 30 Videos
Similar Questions
Knowledge Check
In R3, consider the planes P1:y=0 and P2,x+z=1. Let P3 be a plane, different from P1 and P2 which passes through the intersection of P1 and P2, If the distance of the point (0,1,0) from P3 is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation(s) is/are true?
A2α+β+2γ+2=0B2α−β+2γ+4=0C2α+β−2γ−10=0D2α−β+2γ−8=0Let P1andP2 be two planes containing the lines L2andL2 respectively.
STATEMENT-1 : If P1andP2 are parallel then L1andL2 must be parallel.
and
STATEMENT-2 : If P1andP2 are parallel the L1andL2 may not have a common point.AStatement-1 is True, Statement-2 is true, Statement- is a correct explanation for Statement -1BStatement-1 is True, Statement-2 is true, Statement- is NOT a correct explanation for Statement -1CStatement-1 is True, Statement-2 is FalseDStatement-1 is False, Statement-2 is trueTwo straight lines l1 and l2 cross each other ar point P The line l1 is moving at a speed v1 perpendicular to itself & line l2 is moving at a speed v2 in the similar fashion. The speed of point P is :
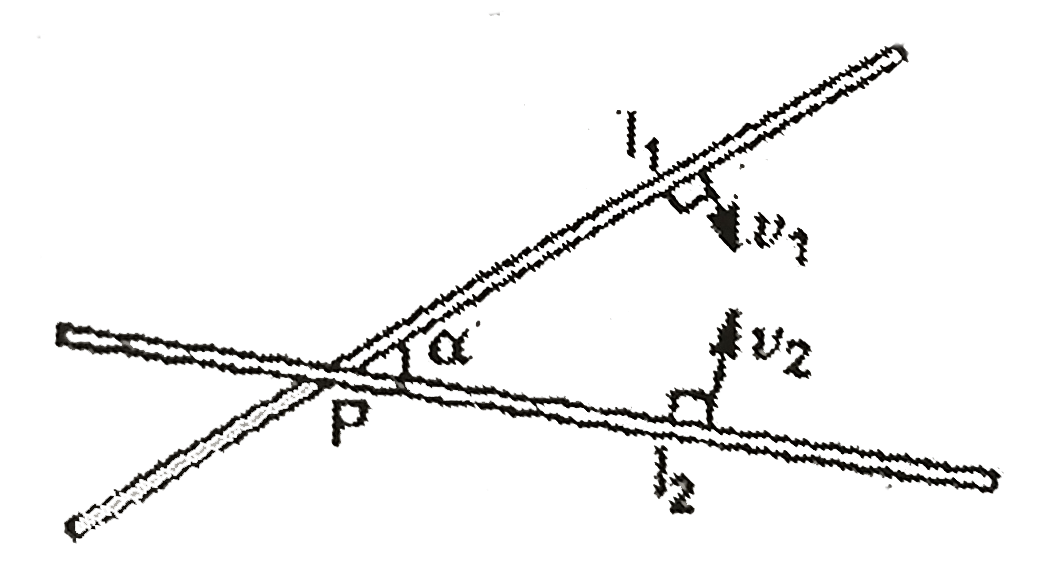 A√v1v2sinαB√v21+v22+2(v1+v2)2cosαcosαC√v21+v22+2(v1+v2)2cosαsinαD(v1+v2)+√v1v2cosαcosα
A√v1v2sinαB√v21+v22+2(v1+v2)2cosαcosαC√v21+v22+2(v1+v2)2cosαsinαD(v1+v2)+√v1v2cosαcosα
Let L1andL2 be two lines intersecting at P If A1,B1,C1 are points on L1,A2,B2,C2,D2,E2 are points on L2 and if none of these coincides with P, then the number of triangles formed by these 8 points is
View SolutionImage of one the other line mirror To find the image of L1=0 through L1=0 first we find the point of intersection of L1=0andL1=0. Let this is B. Again we take a point A on the line L2 and find its image through L1=0, let this is K.
View SolutionA point P is 3units away from line L1=3x+4y+5=0and4 units away from the line L2=8x−by+9=0, The reflection of P on L1, is P1 the reflection of P1 on L2, is P2 the reflection of P3, on L2, is P4, Then the area (in sq. units) of figure formed by joining P1P2P3,andP4, is-
View SolutionConsider three planes P1:x−y+z=1
P2:x+y−z=−1
and P3:x−3y+3z=2
Let L1,L2,L3 be the lines of intersection of the planes P2 and P3,P3 and P1,P1 and P2 respectively.
Statement I Atleast two of the lines L1,L2 and L3 are non-parallel.
Statement II The three planes do not have a common point.
View SolutionConsider the planes p1:2x+y+z+4=0
p2:y−z+4=0andp3:3x+2y+z+8=0
Let L1,I2,I3 be the lines of intersection of the planes P2andP3,P3andP1,P1andP2 respectively. Then:
View Solution
