Question

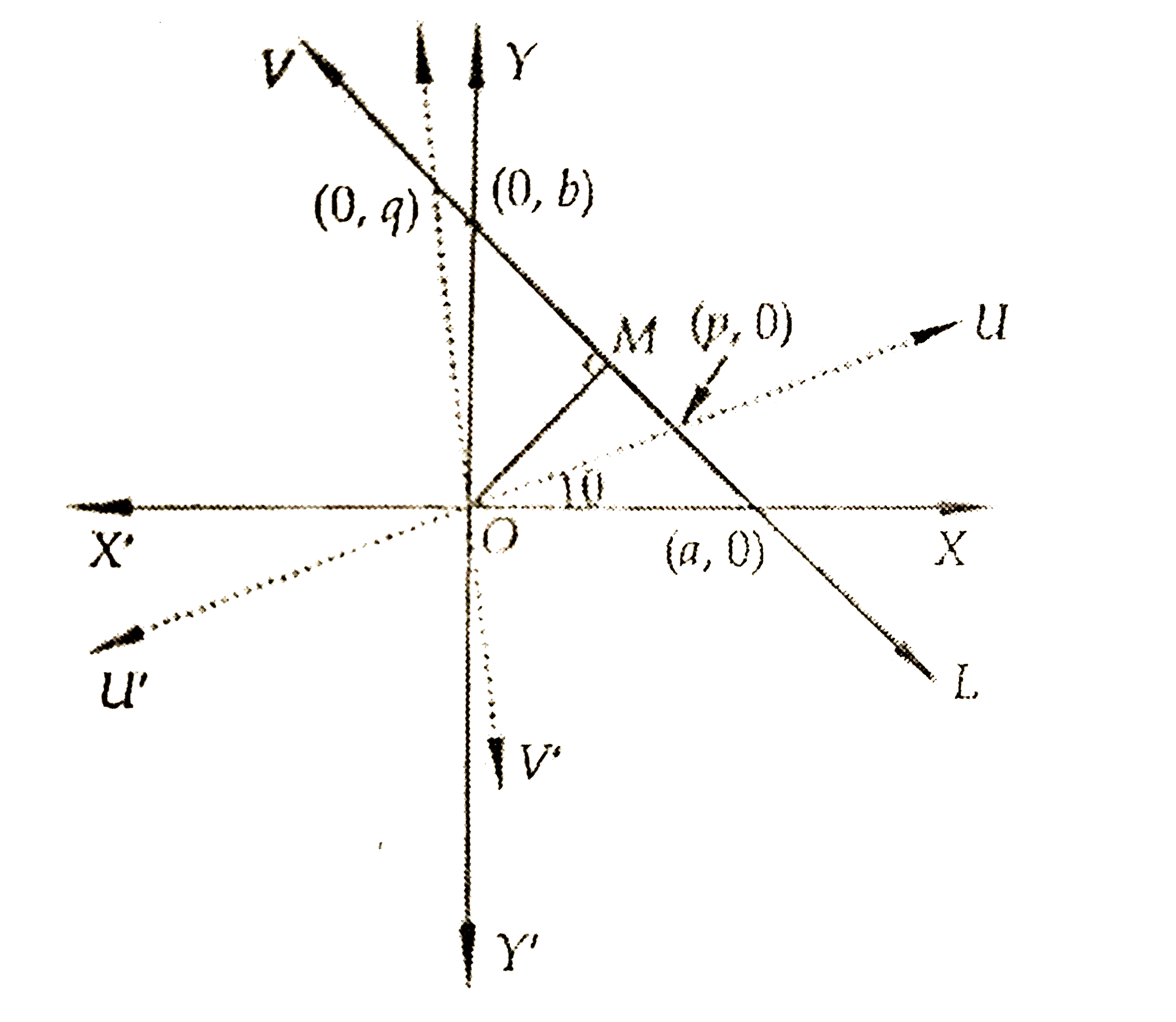
Thu Line L has intercept a and b on the co-ordinate axes. When keeping the origin fixed, the coordinate axis are rotated around a fixed angle, then the line has intercepts p and q on rotate axis, then

Options

A. `a^(2)+b^(2)=p^(2)+q^(2)`
B. `(1)/(a^(2))+(1)/(b^(2))=(1)/(p^(2))+(1)/(q^(2))`
C. `a^(2)+p^(2)=b^(2)+q^(2)`
D. `(1)/(a^(2))+(1)/(p^(2))=(1)/(b^(2))+(1)/(q^(2))`

Answer

B

Explanation

The equation of line L with reference to the old axis is
`(x)/(a)+(y)/(b)=`
OM=Length of the perpendicular from O(0,0) on it
`implies OM =(1)/(sqrt((1)/(a^(2))+(1)/(b^(2))))" "…(i)`
Let the axes be rotated through an angle `theta` . With reference to the new axes, the equation of the line L is
`(x)/(p)+(y)/(q)=1`
`therefore` OM =Length of hte perpendicular from O(0,0) on it
`implies Om=(1)/(sqrt((1)/(p^(2))+(1)/(q^(2))))" "...(ii)`

From (i) and (ii), we get
`(2)/(sqrt((1)/(a^(2))+(1)/(b^(2))))=(1)/(sqrt((1)/(p^(2))+(1)/(q^(2))))implies (1)/(a^(2))+(1)/(b^(2))=(1)/(p^(2))+(1)/(q^(2))`
This is the required relation .
ALITER The equation of the line with reference to the old axes is `(x)/(a)+(y)/(b)=1" "...(i)`
If the axes are rotated through an angle `theta`, then
`x=Xcostheta-Ysin theta, y=Xsin theta+Ycos theta`
here X and Y coordinates of a point P(x,y) with respect to new-axes
The equation of the line with respect to new axes is
`(X)/(p)+(Y)/(q)=1" "(ii)`
Substituting the values of x and y in (i) , we get
`((cos theta)/(a)+(sin theta)/(b))X+((-sin theta)/(a)+(cos theta)/(b))Y=1" "...(iii)`
Clearly, (ii) and (iii) represent the same line . Therefore,
`(1)/(p)=(cos theta)/(a)+(sin theta)/(b) and , (1)/(q)=-(sin theta)/(a) + (cos theta)/(b) `
`implies (1)/(p^(2))+(1)/(q^(2))=(1)/(a^(2))+(1)/(b^(2))`, which is the required relation.