If lines px+qy+r=0,qx+ry+p=0andrx+py+q=0 are concurrent, then prove that p+q+r=0(wherep,q,r are distinct).
A
p+q+r=0
B
p2+q2+r2=pq+qr+rp
C
p3+q3+r3=3pqr
D
none of these
Video Solution
Text Solution
The correct Answer is:C
The lines px+qy+r=0,qx+ry+p=0 and rx+py+q=0 are concurrent, if
∣∣
∣
∣∣pqrqrprpq∣∣
∣
∣∣=0
⇒(p+q+r)2(p2+q2+r2−pq−qr−rp)=0
⇒p3+q3+r3−3pqr=0⇒p3+q3=3pqr
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If x#y=x+yxy, then the value of P#(q#r) for every p, q, in N :
Aa. pq+qr+r2p(q+q+r)Bb. pqr+q+rp(q+r)Cc. p(qr+q+r)pqrDd. None of these
The lines (p−q)x+(q−r)y+(r−p)=0
(q−r)x+(r−p)y+(p−q)=0
(r−p)x+(p−q)y+(q−r)=0
are concurrent
View SolutionProve that pxq−r+qxr−p+rxp−q>p+q+r,wherep,q,r are distinct andx≠1.
View SolutionIf p, q, r are in G.P. and the equations, px2+2qx+r=0and dx2+2ex+f=0have a common root, then show that dp,eq,frare in A.P.
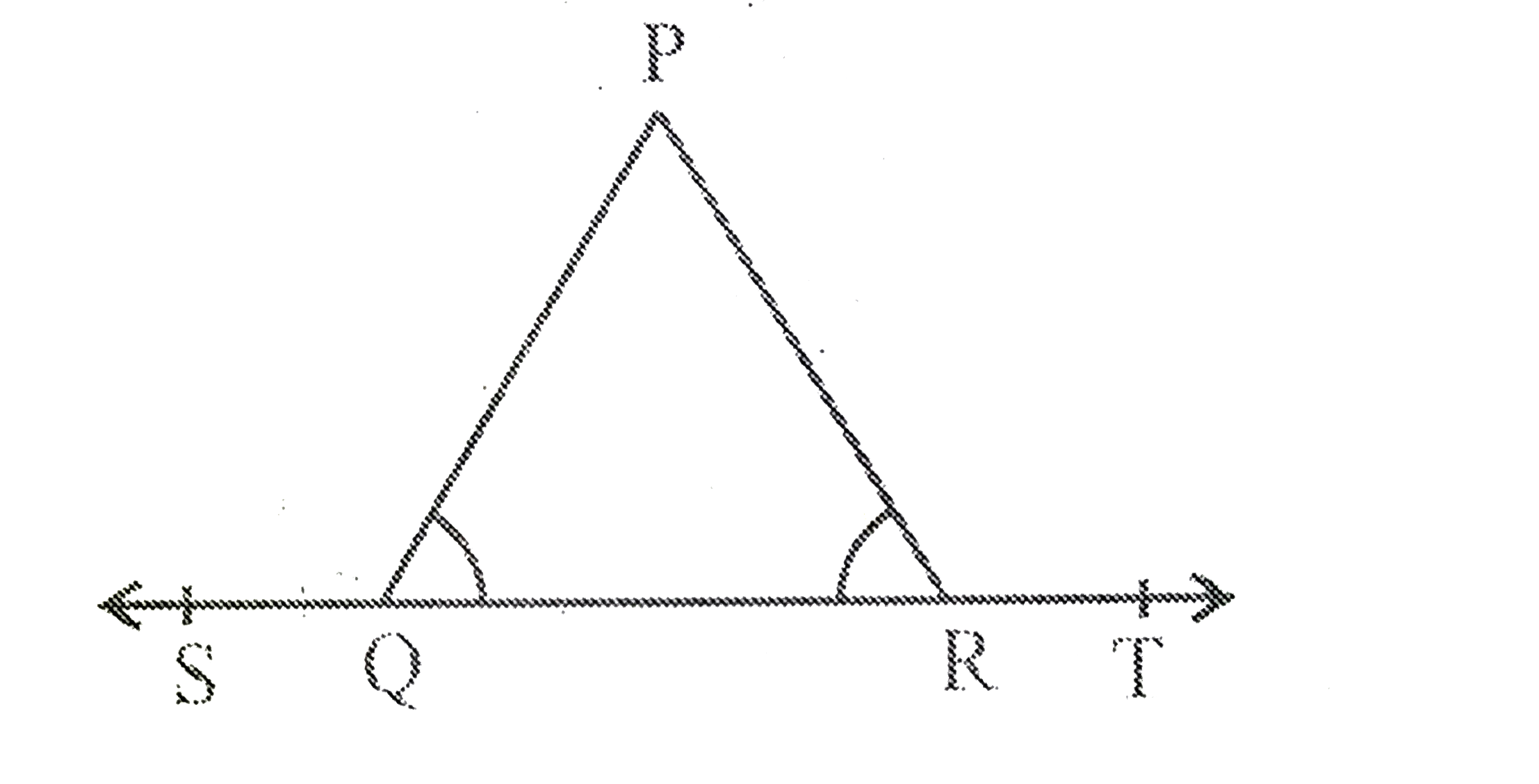
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
View SolutionIf the lines prx+qry+1=0,r=1,2,3 be concurrent then the points (pr,qr),r=1,2,3 are collinear.
View SolutionIf px+qy+r=0andqx+py+r=0(x≠y), then show that the value of x+y is −rpor−rq
View SolutionIf p and q are the roots of the equation x2−15x+r=0 and. p−q=1, then what is the value of r?
View Solution