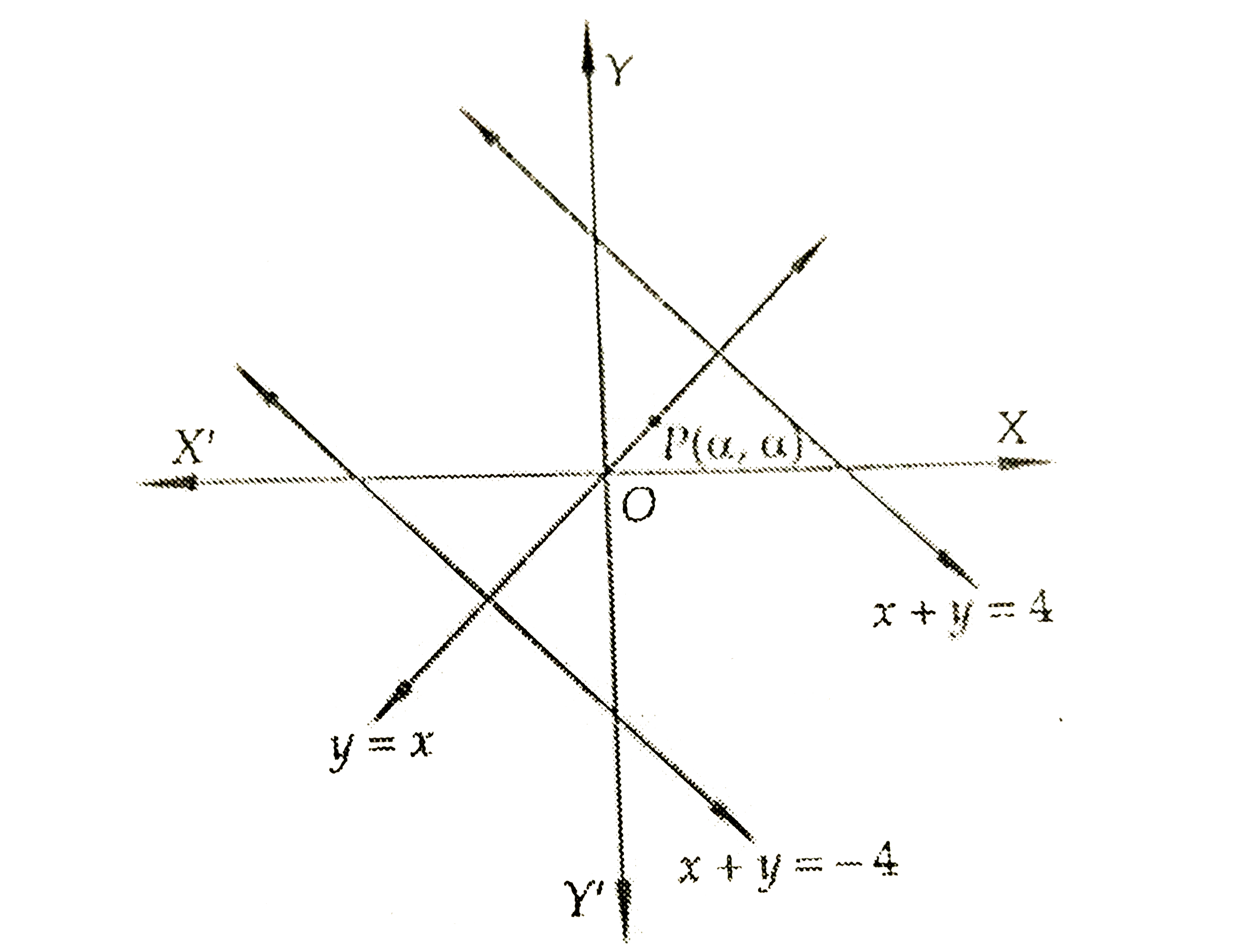
If the point (α,α) falls between the lines |x+y|=4 , then
|α|=4
|α|=2
|α|<2
|α|<4
The correct Answer is:C
The equations of the lines are x+y=4 and x+y=−4 . If (α,α) lies between these lines, then
(α+α−4)(α+α+4)<0
⇒(2α−4)(2α+4)<0⇒(α−2)(α+2)<0⇒|α|<2
Topper's Solved these Questions
Similar Questions
The points (2,1),(3,−2) and (α,β) form a triangle of area 4 square units. If the point (α,β) lies on the line y=x+3, then the value of α+β is (are)
View SolutionThe points (2,1),(3,−2) and (α,β) form a triangle of area 4 square units. If the point (α,β) lies on the line y=x+3 then the value of α+β is (are)
View Solution
Knowledge Check
If the point (a , a) falls between the lines |x + y| = 2. then .
A|a| =2B|a| =1C|a|<1D|a|<12If the point (a,a) falls between the line|x+y|=4, then
A|a|=2B|a|=3C|a|<2D|a|<3The length of perpendicular from the point (acosα,asinα) upon the straight line y=xtanα+c,c>0, is
AcBcsin2αCccosαDcsec2α
The points (2 ,1)(3 ,-2) and (α,β) form a triangle of area 4 square units.If the point (α,β) lies on the line y=x+3 then the value of α+β is (are)
View SolutionThe points (2, 1), (3, -2) and (α,β) form a triangle of area 4 square units.If the point (α,β) lies on the line y=x+3 then the value ofα+β is (are)
View SolutionIf the point (1,α) always remains in the interior of the triangle formed by the lines y=x,y=0andx+y=4, then α lies in the interval
View SolutionThe length of perpendicular from the point (acosα,asinα) upon the straight line y= x tanα+c,c>0, is :
View SolutionThe length of perpendicular from the point (acosα,asinα) upon the straight line y= x tanα+c,c>0, is :
View Solution
