The point (2,1) , translated parallel to the line x−y=3 by the distance of 4 units. If this new position A' is in the third quadrant, then the coordinates of A' are-
(2+2√2,1+2√2)
(−2+√2,−1−2√2)
(2−2√2,1−2√2)
none of these
The correct Answer is:C
Since the point A(2,1) is translated parallel to x−y=3. Therefore, AA' has the same slope as that of x-y=3 . Thus, AA' passes through (2,1) and has the slope =1.
So, the equation of AA' is
x−2cosπ/4=y−1sinπ/4
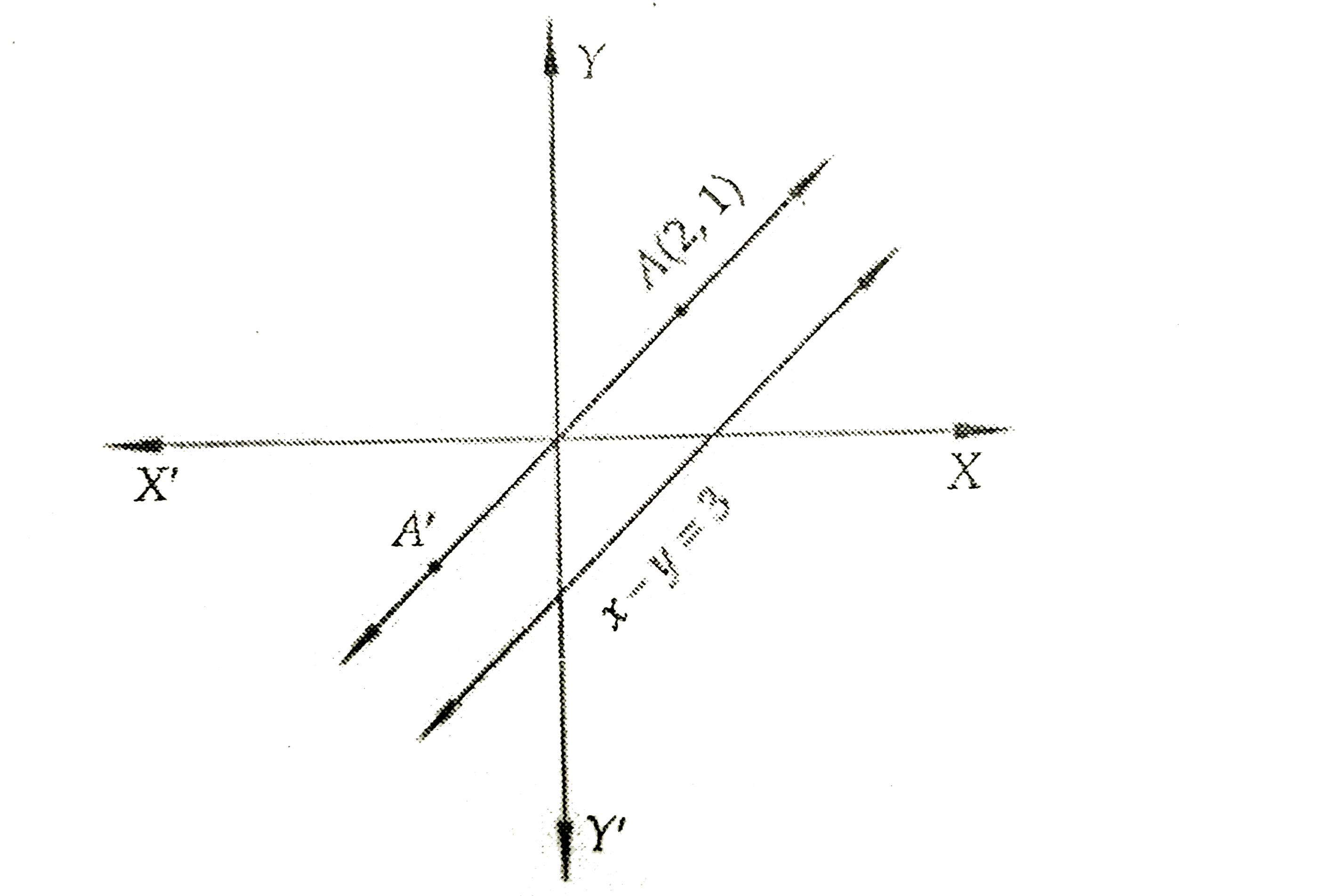
Since, AA'=4 . Therefore , coordinates of A' are given by
x−2cosπ/4=y−1sinπ/4=−4
⇒x=2−4cosπ4,y=1−4sinπ4
⇒x=2−2√2,y=1−2√2.
Hence , the coordinates of A' are (2−2√2,1−2√2)
Topper's Solved these Questions
Similar Questions
The point (2,1) , translated parallel to the line x−y=3 by the distance of 4 units. If this new position A' is in the third quadrant, then the coordinates of A' are-
View SolutionThe point A(2,1) is translated parallel to the line x−y=3 by a distance of 4 units. If the new position A' is in the third quadrant, then the coordinates of A' are (A) (2+2√2,1+2√2 (B) (−2+√2,−1−2√2) (C) (2−2√2 , 1−2√2) (D) none of these
View Solution
Knowledge Check
The point A(2,1) is translated parallel to the line x−y=3 by a distance 4 units. If the new position A' is in third quadrant, then the co ordinates of A' are
A(2+2√2,1+2√2)B(−2+√2,−1−2√2)C(2−2√2,1−2√2)DNone of theseA line parallel to the straight line 3x−4y−2=0and at a distance of 4 units from it is
A3x−4y+20=0B4x−3y+12=0C3x−4y+18=0D3x−4y−22=0The point P(1,1) is translated parallel to 2x=y in the first quadrant through a unit distance. The coordinates of the new position of P are
A(1±2√5,1±1√5)B(1±1√5,1±2√5)C(1√5,2√5)D(2√5,1√5)
The point (2,1) is translated parallel to the line L:x−y=4 by 2√3units. If the new point Q lies in the third quadrant, then the equation of the line passing through Q and perpendicular to L is
View SolutionThe point P(1,1) is translated parallal to the line 2x=y in the first quadrant through a unit distance.The coordinates of the new position of P are:
View SolutionThe point P(1,2,3) is shifted parallel to the line x−33=y−24=z−312 by distance 13 units. Then the new coordinates of P in new position can be
View SolutionThe eq. of the lines parallel to 4x+3y+2=0 and at a distance of '4' units from it are
View SolutionIf a point P(4,3) is shifted by a distance √2 unit parallel to the line y=x, then coordinates of P is new position are
View Solution
