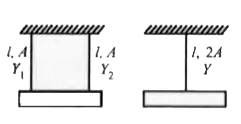
Two wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be

Y1+Y2
Y1+Y22
Y1Y2Y1+Y2
√Y1Y2
The correct Answer is:B
Y=FA×lΔl
Spring constant of wire
k=FΔl=YAl
keq=k1+k2
or Y(2A)l=Y1Al+Y2Al or Y=Y1+Y22
Topper's Solved these Questions
- BULK PROPERTIES OF MATTERBook:MTG-WBJEEChapter:BULK PROPERTIES OF MATTERExercise:WB JEE WORKOUT (ONE OR MORE THAN ONE OPTION CORRECT TYPE )
Explore 10 Videos
- BULK PROPERTIES OF MATTERBook:MTG-WBJEEChapter:BULK PROPERTIES OF MATTERExercise:WB JEE PREVIOUS YEARS QUESTIONS (SINGLE OPTION CORRECT TYPE)
Explore 22 Videos
- ATOMS MOLECULES AND CHEMICAL ARITHEMETIC Book:MTG-WBJEEChapter:ATOMS MOLECULES AND CHEMICAL ARITHEMETIC Exercise:WB JEE PREVIOUS YEARS QUESTIONS CATEGORY 1: SINGLE OPTION CORRECT TYPE (1 MARK)
Explore 3 Videos
- CURRENT ELECTRICITY Book:MTG-WBJEEChapter:CURRENT ELECTRICITY Exercise:WB JEE PREVIOUS YEARS QUESTIONS
Explore 21 Videos
Similar Questions
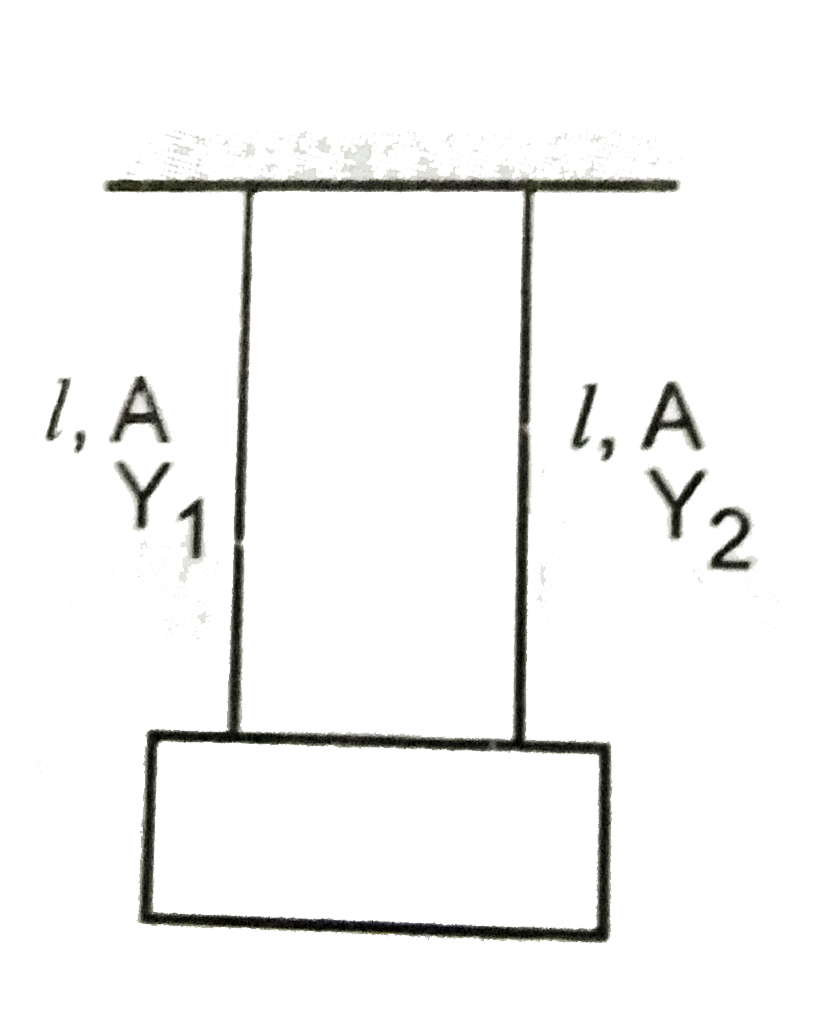
Two wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
View SolutionTwo wires of equal length and cross sectional area suspended as shown in
Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View Solution
Knowledge Check
Two wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
 AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2
AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2Three vertical wires, I,II and III are supporting a block of mass M in horizontal positon. The wires are to equal length and cross-sectional area. It is given that Young's modulus of wire II,Y2=Y3 (Yong's modulus of wire III). The wire I and III and attached at extreme ends of the block.
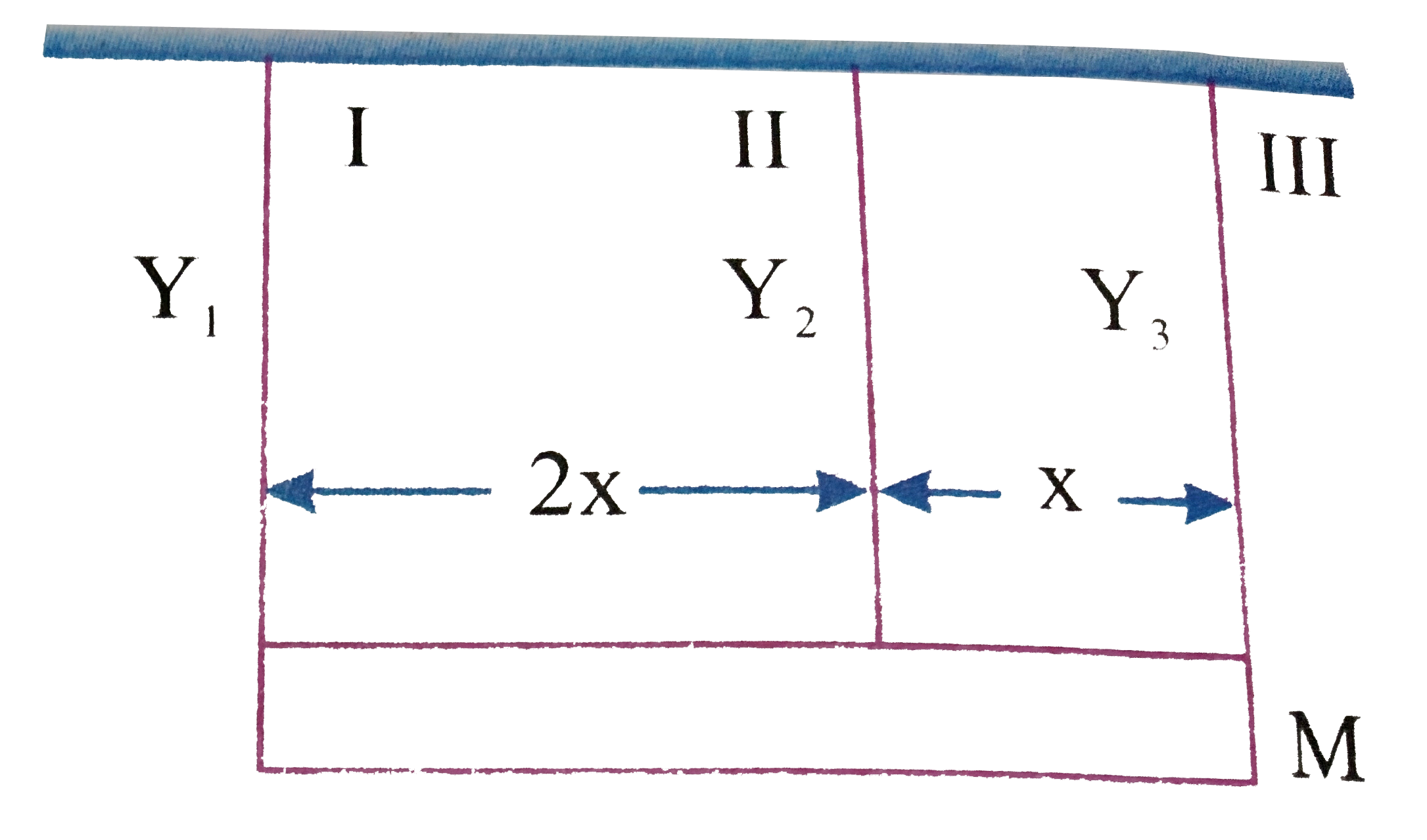 AT1=2T3B2T1=T3CT2=T3DT1=Mg/5
AT1=2T3B2T1=T3CT2=T3DT1=Mg/5The elastic enery stored in a wire of Young's modulus Y is
AY×Strain2VolumeBStress × Strain × VolumeCStress2×Volume2YD12Y× stress × Strain × Volume
A horizontal rod suspended from two wires of same length and cross - section. Their Young's modulus are Y1 and Y2 respectively. The equivalent Young's modulus will be

View SolutionTwo wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
View SolutionA wire having a length L and cross- sectional area A is suspended at one of its ends from a ceiling . Density and young's modulus of material of the wire are ρ and Y, respectively. Its strain energy due to its own weight is ρ2g2AL3αY. Find the value of α
View SolutionTwo wires of equal dimensions and young's modulus Y1 and Y2 are connected end to end. What is the equivalent young's modulus for the combination?
View SolutionA wire of length L and cross-sectional area A is made of material of Young's modulus Y. The work done in stretching the wire by an amount x is
View Solution
