The equation of the parabola with vertex at the origin passing through (2,3) and the axis along x-axis is
Video Solution
Text Solution
It is given that the vertex of the parabola is O(0,0) and it is symmetric about the x-axis, So, its equation is y2=4ayory2=−4ax. Since it passes through the point P(2,3), so it is lies in the first quadrant.
∴ it is a right-handed parabola.
So, its equation is y2=4ax
Now, P(2,3) lies on it, so 32=4a×2⇒a=98 Hence, the required equation is y2=98x⇒y2=92x.
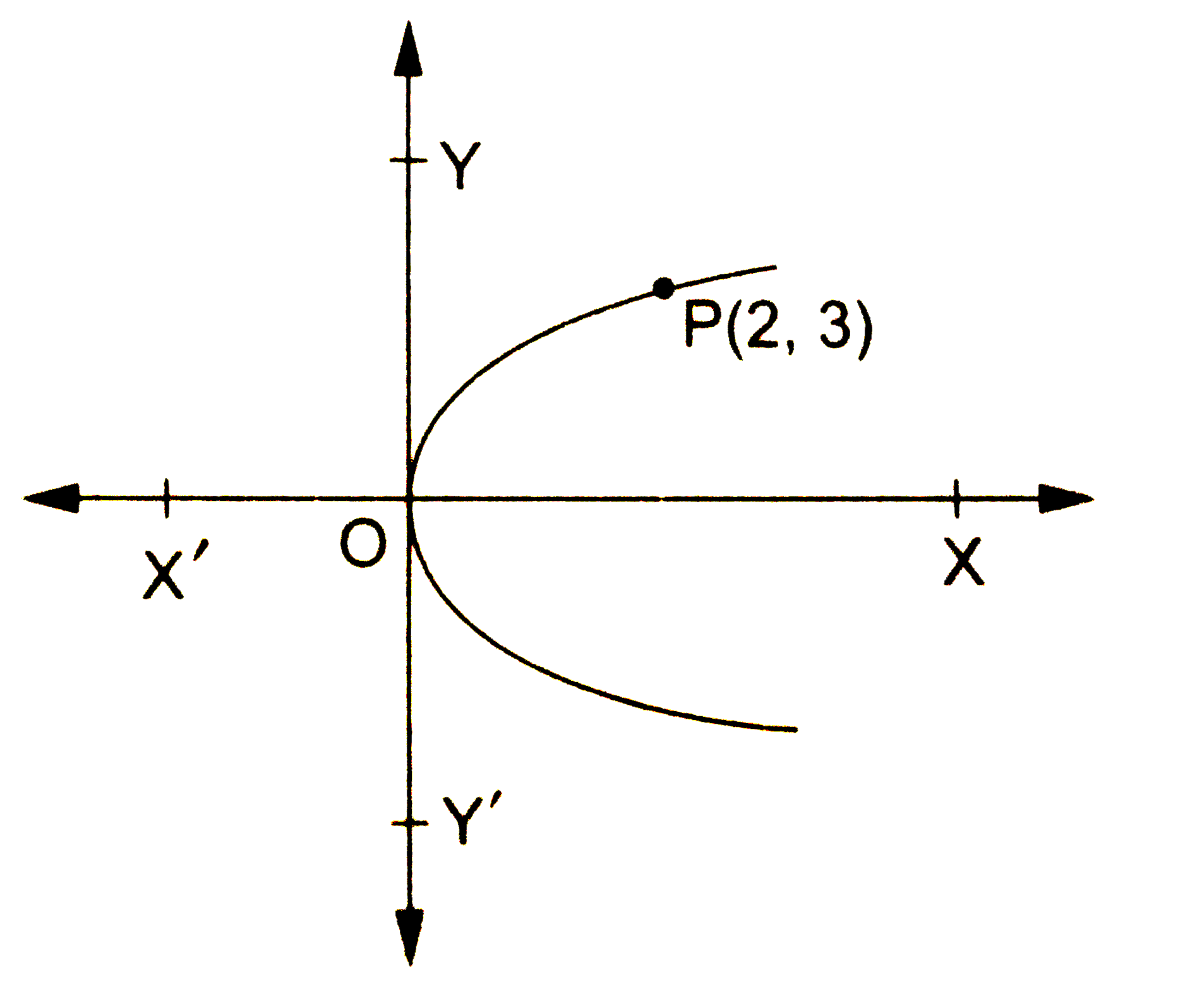
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the equation of the parabola with vertex (0,0) and passing through (2,3) and axis is along the x-axis.
Ax2=92yBy2=92xCy2=92xDx2=−92yThe equatio of the parabola with its vertex at the origin, axis on the Y-axis and passing through the point (6,−3) is
Ay2=12x+6Bx2=12yCx2=−12yDy2=−12x+6
Vertex (0, 0) passing through (2,3) and axis is along x-axis.
View SolutionFind the equation of the parabola with vertex at the origin, passing throgh the point P(3,-4) and symmetric about the y-axis.
View SolutionThe equation of the directrix of the parabola with vertex at the origin and having the axis along the x-axis and a common tangent of slope 2 with the circle x2+y2=5 is (are) (a)x=10 (b) x=20 (c)x=−10 (d) x=−20
View SolutionFind the equation of the line passing through (-2,-3) and
parallel to x-axis
View SolutionFind the equation of the parabola with vertex at origin, symmetric with respect to y-axis and passing through (2,−3)
View SolutionFind the equation of the parabola that satisfies the given conditions:Vertex (0,0) passing through (2,3) arid axis is along x–axis.
View Solution