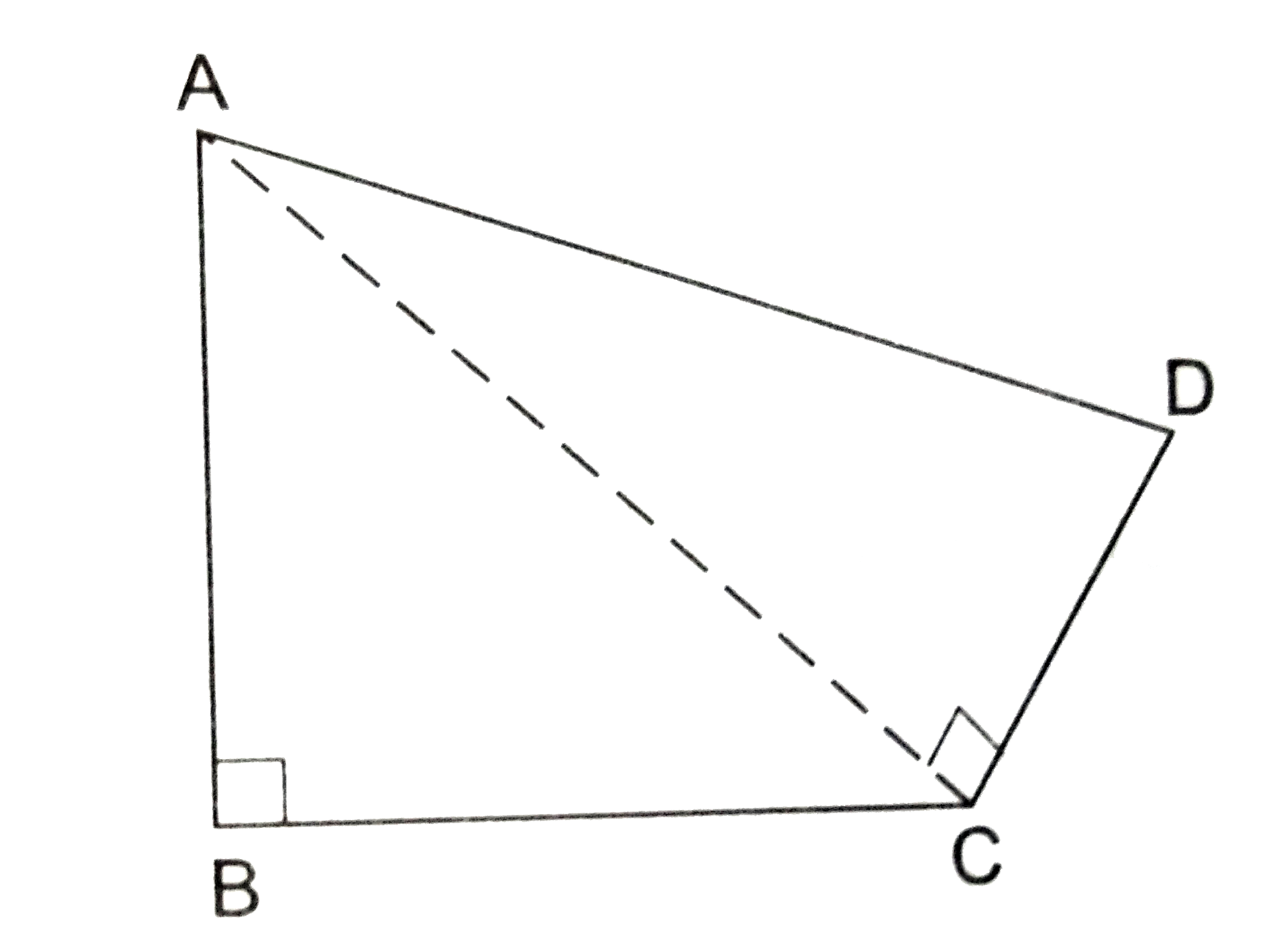
In a quadrilateral ABCD, ∠B=90∘andAD2=AB2+BC2+CD2 prove that ∠ACD=90∘ .
GIVEN A quad. ABCD in which ∠B=90∘andAD2=AB2+BC2+CD2.
PROVE ∠ACD=90∘
CONSTRUCTION Join AC.
PROOF In ΔABC,∠B=90∘
∴AC2=AB2+BC2 ....(i) [ by Pythagora's theorem] ltbr Now, AD2=AB2+BC2+CD2 ( givem) ltbr ⇒AD2=AC2+CD2 [ using (i)]
Thus, in ΔACD , we have AD2=AC2=AC2+CD2
Hence,∠ACD=90∘[ by converse of Pythagora's theorem]
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
In a quadrilateral ABCD, ∠B=90o . If AD2=AB2+BC2+CD2 then prove that ∠ACD=90o .
View SolutionIn the figure ∠B=90∘,
AD2=AB2+BC2+CD2.
Prove ∠ACD=90∘ .
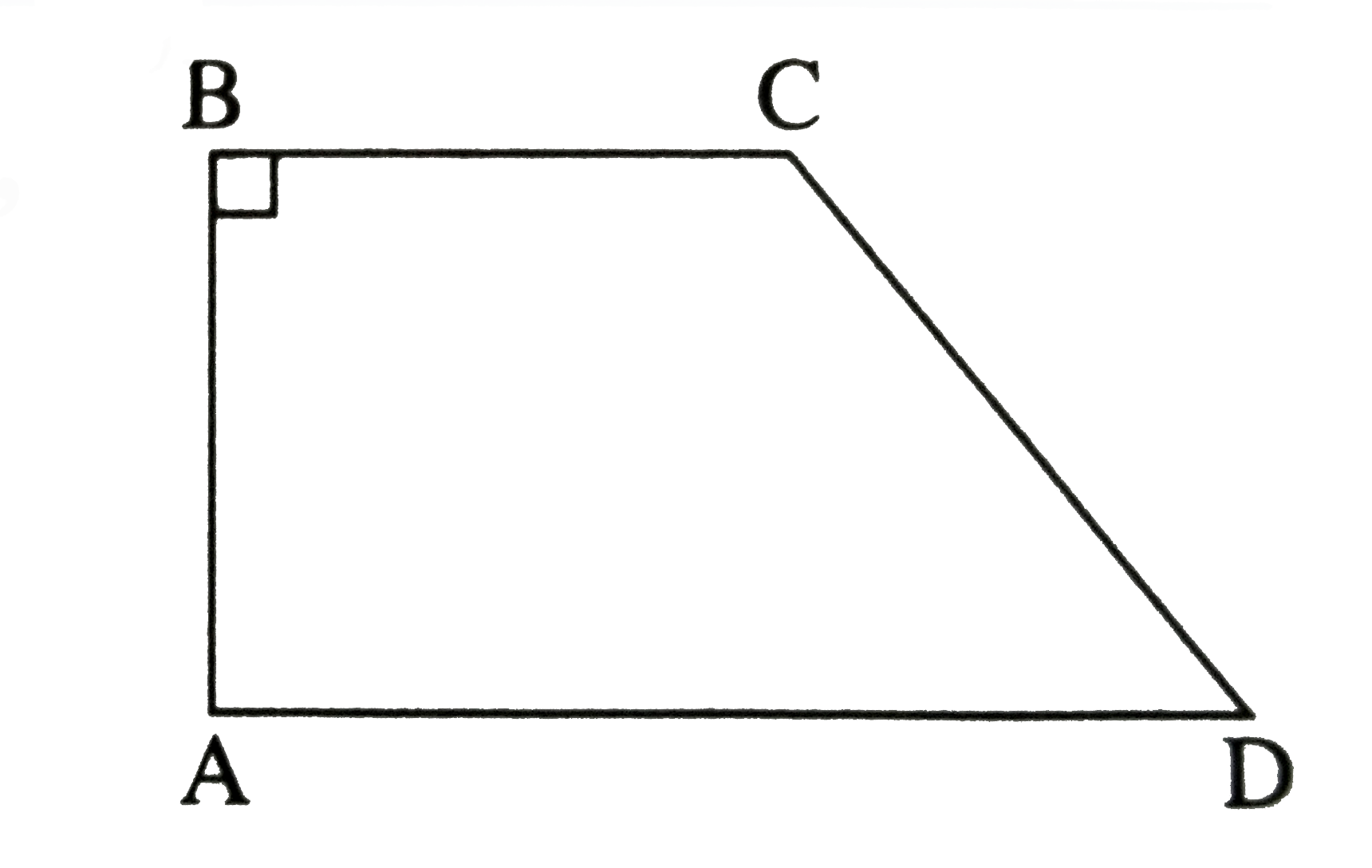
View SolutionIn a quadrilateral ABCD , ∠B=90o , AD2=AB2+BC2+CD2 , prove that ∠ACD=90o
View SolutionIn a quadrilateral ABCD, ∠A+∠D=90∘. Prove that
AC2+BD2=AD2+BC2
View SolutionIn a quadrilateral ABCD, ∠A+∠D=90∘. Prove that AC2+BD2=AD2+BC2.
View SolutionIn a ΔABC,∠B=90∘andAC=8√2. If AB=BC, then find AB.
View SolutionIn a quadrilateral ABCD, show that (AB+BC+CD+DA)<2(BD+AC).
View SolutionIn the given quadrilateral ABCD,AB=15cm,BC=20cmandAD=7cm∠ABC=∠ADC=90∘. Find the length of side CD:
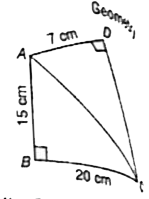
View SolutionIn a quadrilateral ABCD prove that AB2+BC2+CD2+DA2=AC2+BD2+4PQ2 where P and Q are middle points of diagonals AC and BD.
View SolutionIn a quadrilateral ABCD, prove that AB2+BC2+CD2+DA2=AC2+BD2+4PQ2, where P and Q are middle points of diagonals AC and BD.
View Solution