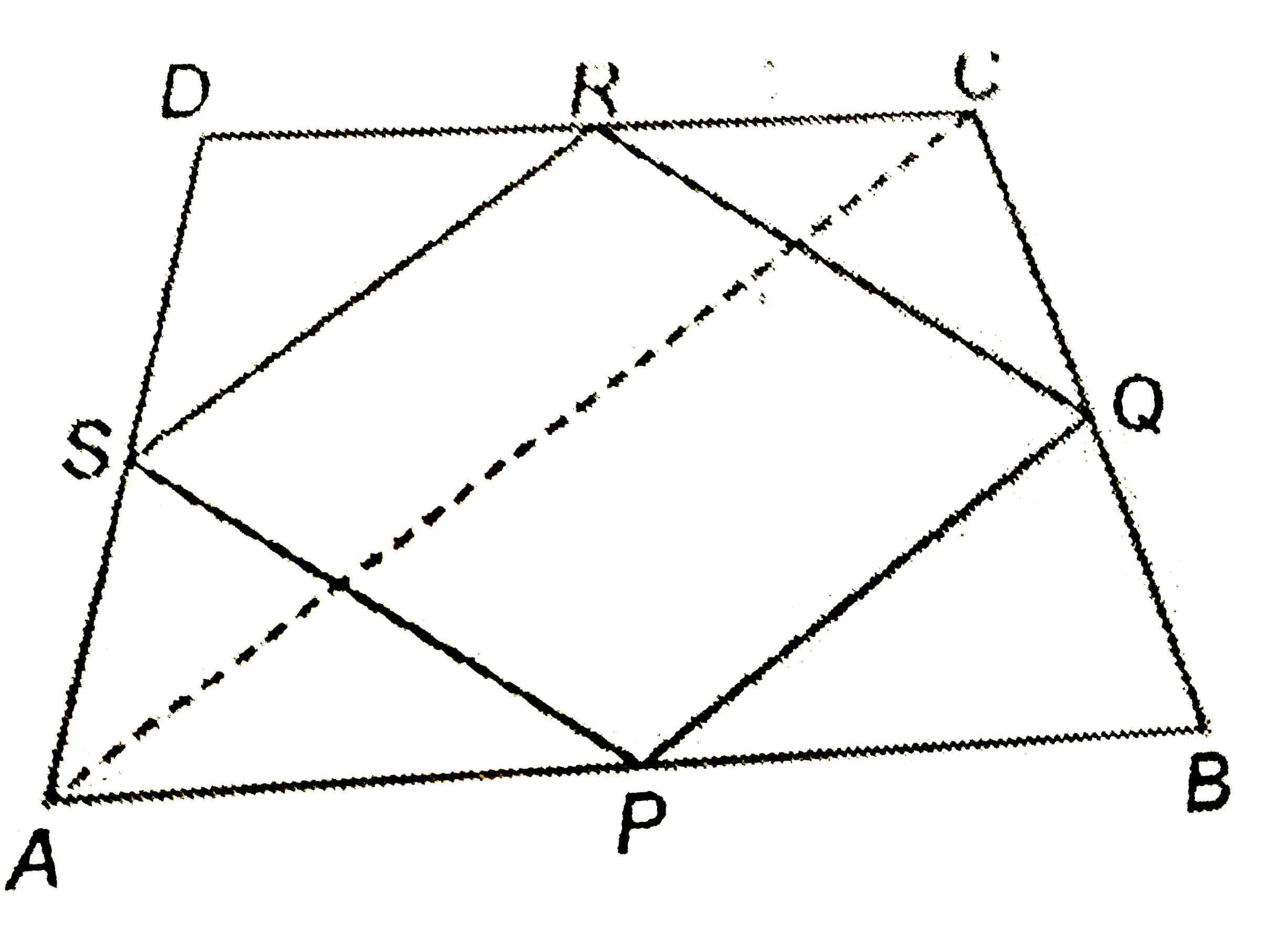
Prove that the line segments joints joining the mid-points of the adjacent sides of a quadrilateral from a parallelogram.
GIVEN A quadrilateral ABCD in which P,Q,R,S are the midpoint of AB,BC, CD and DA respectively.
TO PROVE PQRS is a parallelogram .
CONSTRUCTION Join AC.

PROOF In ΔABC,PandQ are the midpoints of AB and BC respectively.
∴PQ∣∣AC ...(i) [ by midpoint theorem]
In ΔDAC,SandR are the midpoints of AD and CD respecrtively.
∴PQ∣∣AC ...(ii) [ by midpoint theorem]
From (i) and (ii), we get PQ∣∣QR.
Similarly by joining BD, we can prove that PS∣∣QR.
Here, PQRS i a parallelogram.
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Using vector method, prove that the line segments joining the mid-points of the adjacent sides of a quadrilateral taken in order form a parallelogram.
View SolutionProve that the figure formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View Solution
Knowledge Check
The line segments joining the midpoints of the adjacent sides of a quadrilateral form
Aa parallelogramBa rectangleCa squareDa rhombusThe meeting point of adjacent sides of a quadrilateral is called a___
AVertexBSideCcornerDSegment
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View SolutionThe figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a parallelogram (b) rectangle square (d) rhombus
View SolutionThe figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a parallelogram (b) rectangle (c) square (d) rhombus
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View Solution