The line segment joining the mid-points of any two sides of a triangle is parallel to the third side of a triangle.
Video Solution
Text Solution
GIVEN AΔABC in which D and E are the midpoint of AB and AC respectively
TO PROVE AE∣∣EC.
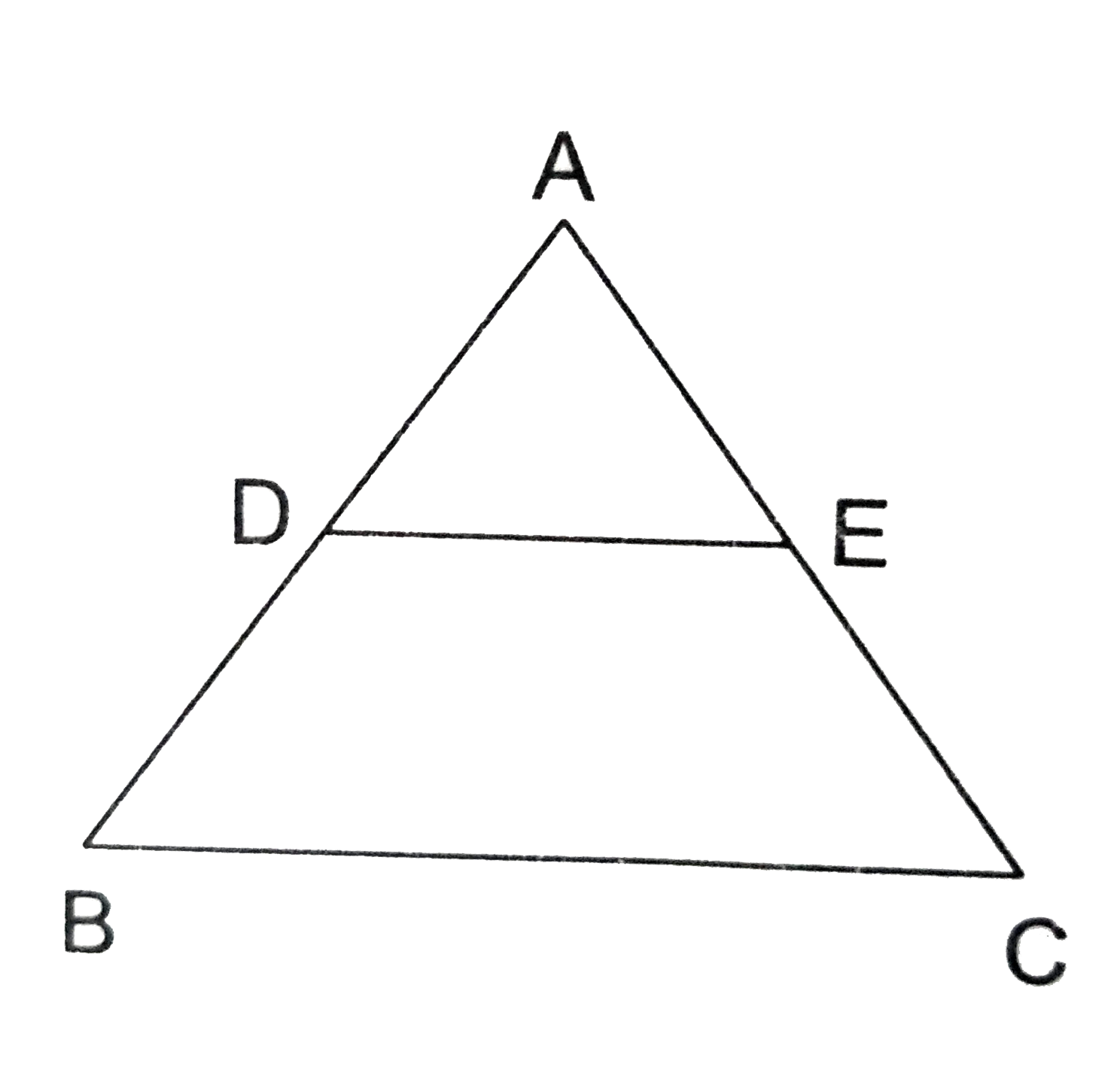
PROOF Since D and E are the midpoints of AB and AC resepctively, we have AD=DB and AE=EC.
∴ADDB=AEEC [ each equal to 1]
Hence, by the converse of Thale's theorem , DE∣∣BC.
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
Assertion : ABCD and PQRC are rectangles and Q is a midpoint of AC. Then DP = PC.
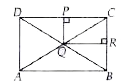
Reason : The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.
In the given figure, the side AC of ΔABC is produced to E such that CE = FAC. If D is the midpoint of BC and ED produced meets AB at F and CP, DQ are drawn parallel to BA, then FD=
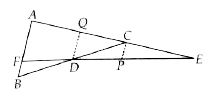 A12FEB13EFC2FEDFE
A12FEB13EFC2FEDFEAssertion : If a line divides any two sides of a triangle in the same ratio , then the line is paralle to third side .
Reason : Line segment joining the mid -point of any two sides of a triangle is parallel to the third side .AIf both assertion and reason are true and reason is the correct explanation of assertion .BIf both assertion and reason are true but reason is not the correct explanation of assertion .CIf assertion is true reason is false .DIf assertion is false but reason is true .
Prove that the line segment joining the mid points of two side of a triangle is parallel to the third side and equal to half of it.
View Solutionprove that the line segment joining the mid-points of two sides of a triangle is parallel to the third side.
View SolutionProve that the line segment joining the mid points of two sides of a triangle is parallel to its third side.
View SolutionProve that the line joining the mid-points of the two sides of a triangle is parallel to the third side.
View SolutionUsing Theorem 6.2, prove that the line joining the mid-point of any two sides of a triangle is parallel to the third side. (Recall that you have done it in class IX).
View Solution
