ABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that $\frac{A O}{O C} = \frac{B O}{O D}$

Video Solution

Text Solution

Verified by Experts

GIVEN A trapezium ABCD in which $A B ∣ ∣ C D$ and its diagonals AC and BD intersect at O.
TO PROVE $\frac{A O}{O C} = \frac{B O}{O D}$
CONSTRUCTION Through O, draw $E O ∣ ∣ A B$ , meetng AD at E.

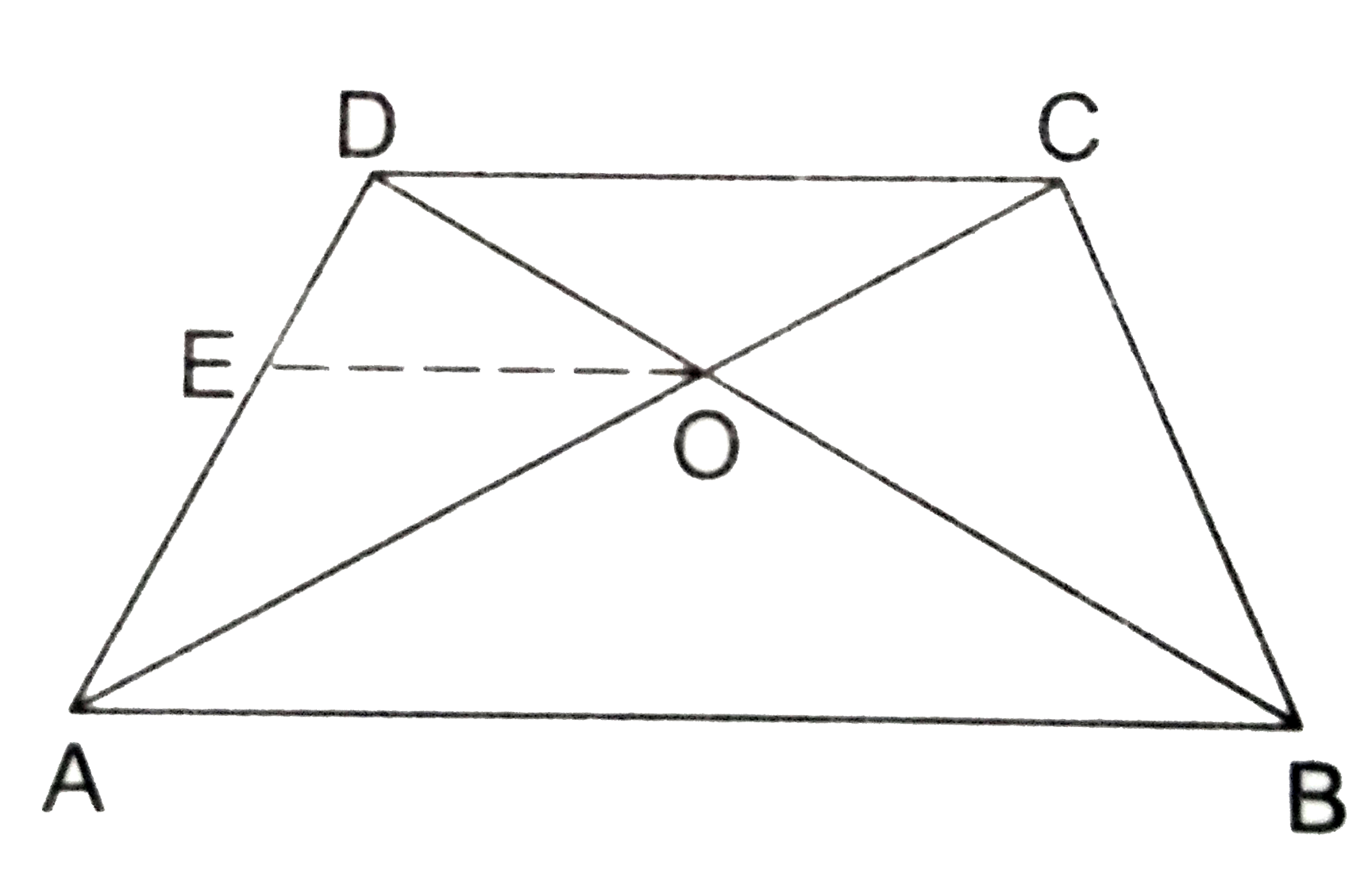
PROOF In $Δ A D C, E O ∣ ∣ D C [∴ E O | | A B | | D C]$
$∴ \frac{A E}{E D} = \frac{A O}{O C} ... . . (i)$ [ by Thale's theorem]
In $Δ D B A, E O ∣ ∣ A B$ .
$∴ \frac{D E}{E A} \frac{D O}{O B}$ [ by Thale's theorem]
$\Rightarrow n \frac{A E}{E D} = \frac{B D}{O D} ... . . (i i)$
From (i) and (ii), we get
$\frac{A O}{O C} = \frac{B O}{O D}$

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
ABCD is a regular trapezium in which $A D ∣ ∣ B C$ Diagonal AC and BD intersect at O, AO = 3 CO = X - 3 BO = 3X - 19 , DO = X - 5 . Find X
A $- 8, 9$
B $8, - 9$
C $- 8, - 9$
D $8, 9$
Question 2 - Select One
ABCD is a trapezium in which $A B ∣ ∣ C D$ and $A B = 2 C D$ . It its diagonals intersect each other at O then ratio of the area of triangle AOB and COD is
A $1 : 2$
B $2 : 1$
C $1 : 4$
D $4 : 1$
Question 3 - Select One
ABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
A $1 : 4$
B $1 : 2$
C $4 : 1$
D $2 : 1$

RS AGGARWAL-TRIANGLES-Test Yourself

Home
Ask Doubt
Profile