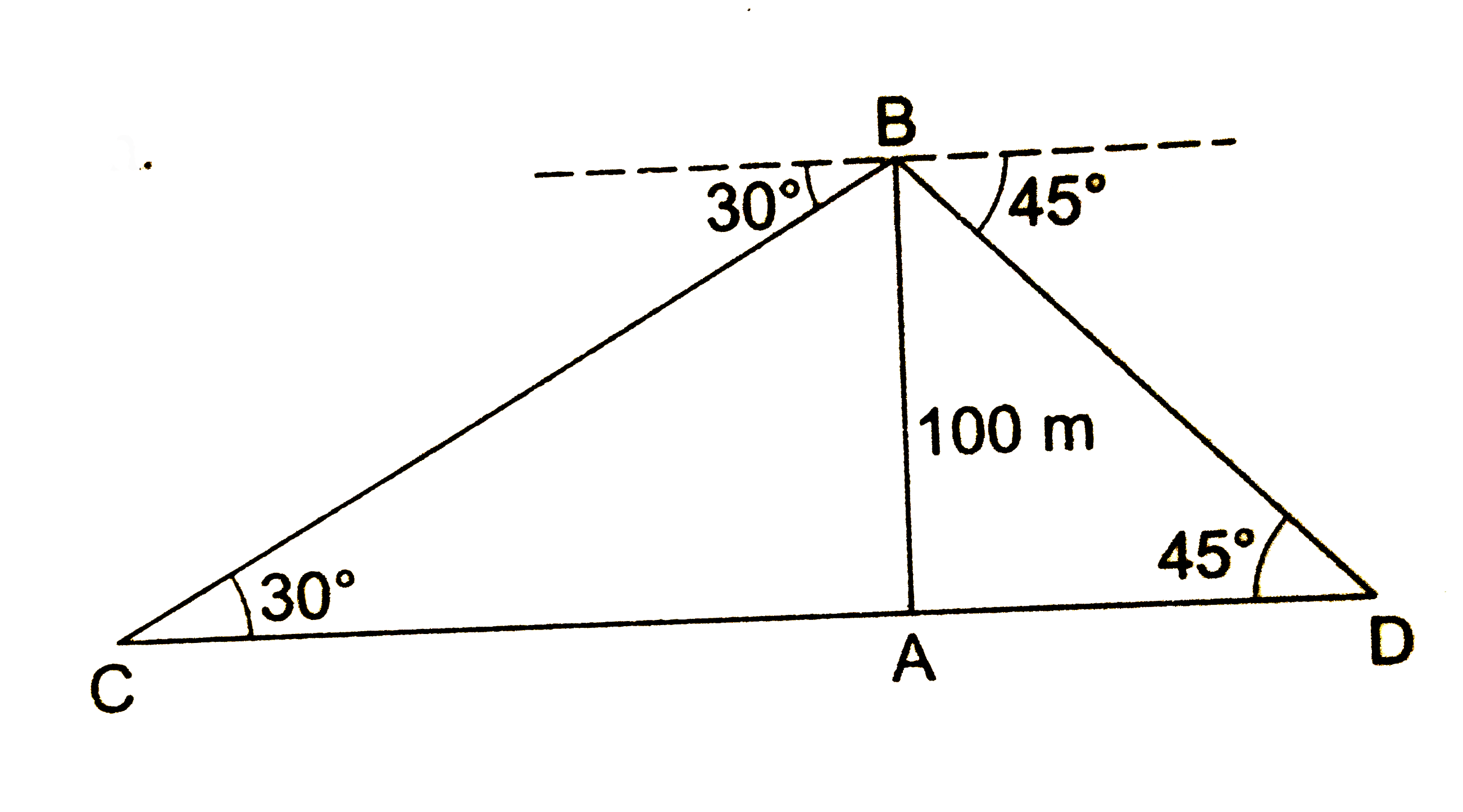
From the top of a tower $100 m$ high, a man observes two cars on the opposite sidesof the tower and in same straight line with itsbase, with angles of depressoin $30^{\circ}$ and $45^{\circ}$ respectively. Find the distance between the cars . [Take $\sqrt{3} = 1.732$ ]

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $273.2 m$

From right $Δ B A D$ , we have
$\frac{A D}{A B} = {cot 45}^{\circ} = 1 \Rightarrow \frac{A D}{100 m} \Rightarrow A D = 100 m$ .
From right $Δ B A C$ , we have
$\frac{A C}{A B} = {cot 30}^{\circ} = \sqrt{3} \Rightarrow \frac{A C}{100 m} = \sqrt{3}$ .
$\Rightarrow A c = (100 \times 1.732) m = 173.2 m$ .
$∴$ distance between the cars.
$= (173.2 + 100) m = 273.2 m$ .

|

Updated on:21/07/2023

Class 10 MATHS SOME APPLICATIONS OF TRIGONOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An observer standing on a 300 m high tower observes two boats in the same direction, their angle of depression are $60^{\circ} and 30^{\circ}$ respectively. The distance between the boats is
A173.2 m
B346.4 m
C25 m
D72 m
Question 2 - Select One
A straight highway leads to the foot of a tower of height 50 m. From the top of tower, the angles of depression of two cars standing on the highway are $30^{\circ}$ and $60^{\circ}$ respectively. What is the distance between the two cars and how far is each car from the tower?
A $\frac{100}{\sqrt{3}} m$
B $100 \sqrt{3} m$
C86.50 m
DNone of these
Question 3 - Select One
Two men are on opposite sides of a tower .They measure the angles of elevation of the top of the tower as $30^{\circ} and 45^{\circ}$ respectively .If the height of the tower is 50 metre , the distance between the two men is (Take $\sqrt{3} = 1.73)$
A136.5 metre
B $50 \sqrt{3}$ metre
C $100 \sqrt{3}$ metre
D $135 .5$ metre

RS AGGARWAL-HEIGHTS AND DISTANCES-Exercise 14

Home
Ask Doubt
Profile