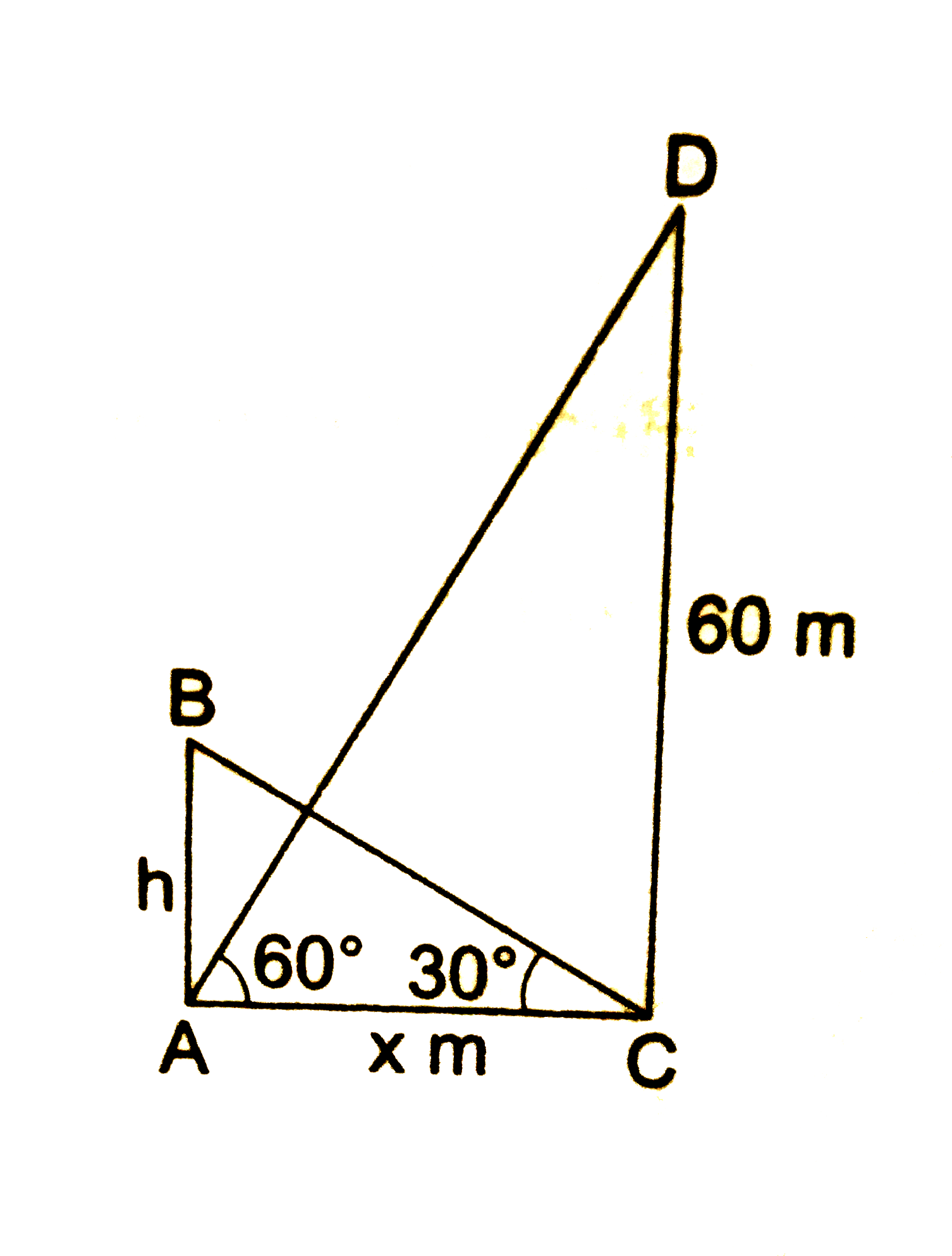
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
The correct Answer is:20 m
Let AB be the building and CD be the tower.
From right ΔACD , we have
ACAD=cot60∘=1√3⇒x60=1√3⇒x=60√3.
⇒x=60√3×√3√3=20√3.
From right ΔBAC, we have
ABAC=tan30∘⇒hx−1√3⇒h=x√3.
h=20√3√3=20√3.
Topper's Solved these Questions
- HEIGHTS AND DISTANCESBook:RS AGGARWALChapter:HEIGHTS AND DISTANCESExercise:Multiple Choice Questions (Mcq)
Explore 25 Videos
- HEIGHTS AND DISTANCESBook:RS AGGARWALChapter:HEIGHTS AND DISTANCESExercise:Multiple Choice Questions (Mcq)
Explore 25 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Multiple Choice Questions (Mcq)
Explore 34 Videos
- LINEAR EQUATIONS IN TWO VARIABLES Book:RS AGGARWALChapter:LINEAR EQUATIONS IN TWO VARIABLES Exercise:QUESTION
Explore 2 Videos
Similar Questions
The angle of elevation of the top of a building from the foot of the tower is 30∘ and the angle of elevation of the top of tower from the foot of the building is 60∘,If the tower is 50 m high, find the height of the building.
View SolutionThe angle of elevation of the top of a building from the foot of the tower is 30∘and the angle of elevation of the top of the tower from the foot of the building is 60∘. If the tower is 50 m high, find the height of the building.
View Solution
Knowledge Check
The angle of elevation of the top of a hill from the foot of a tower is 60∘ and the angle of elevation of the top of the tower from the foot of the hill is 30∘. If the tower is 50 m high, then what is the height of the hill?
A180 mB150 mC100 mD120 mThe angle of elevation of the top of a hill at the foot of a tower is 60∘ and hte angle of elevation of the top of the tower form the foot of the hill is 30∘ . If the tower is 50 m high, what is the hight of the hill
A1350 mB1268 mC1000 mD1160 mThe angle of elevation of the top of a hill from the foot of a tower is 60∘ and the angle of elevation of the top of the tower from the foot of the hill is 30∘. If the tower is 50 m high, then what is the height of the hill?
A100√3mB50√3mC150mD150√3m
The angle of elevation of the top of a building from the foot of a tower is 30∘ . The angle of elevation of the top of the tower from the foot of the building is 60∘ . If the tower is 60 m high, find the height of the building.
View SolutionThe angle of elevation of the top of a building from the foot of the tower is 30∘ and the angle of elevation of the top of the tower from the foot of the building is 45∘. If the tower is 30 m high, find the height of the building.
View SolutionThe angle of elevation of the top of a building from the foot of tower is 30∘ and the angle of elevation of the top of the tower from the foot of the building is 60∘. It the tower is 30 m high, then the height of the building is
View SolutionThe angle of elevation of the top of the building from the foot of the tower is 30o and the angle of the top of the tower from the foot of the building is 60o . If the tower is 50m high, find the height of the building.
View SolutionThe angle of elevation of the top of a hill at the foot of a tower is 60o and the angle of elevation of the top of the tower from the foot of the hill is 30o . If the tower is 50 m high, what is the height of the hill?
View Solution