In the following, state whether A=Bor not:(i) A={a,b,c,d} B={d,c,b,a}(ii) A={4,8,12,16} B={8,4,16,18}(iii) A={2,4,6,8,10} B = {x: x is po
To determine whether the sets A and B are equal in each part of the question, we need to check if they contain the same elements. Two sets are considered equal if they have exactly the same elements, regardless of the order in which they are listed.
Let's analyze each part step by step.
Part (i)
Given:
- A={a,b,c,d}
- B={d,c,b,a}
Step 1: Compare the elements of both sets.
- Set A contains: a,b,c,d
- Set B contains: d,c,b,a
Step 2: Check if both sets have the same elements.
- Both sets contain the elements a,b,c,d.
Conclusion: Since both sets have the same elements, we can conclude that A=B.
Part (ii)
Given:
- A={4,8,12,16}
- B={8,4,16,18}
Step 1: Compare the elements of both sets.
- Set A contains: 4,8,12,16
- Set B contains: 8,4,16,18
Step 2: Check if both sets have the same elements.
- Set A has the element 12 which is not present in Set B.
- Set B has the element 18 which is not present in Set A.
Conclusion: Since the sets do not contain the same elements, we can conclude that A≠B.
Part (iii)
Given:
- A={2,4,6,8,10}
- B={x:x is a positive even integer and x<10}
Step 1: Identify the elements of Set B.
- The positive even integers less than 10 are: 2,4,6,8.
Step 2: Compare the elements of both sets.
- Set A contains: 2,4,6,8,10
- Set B contains: 2,4,6,8
Step 3: Check if both sets have the same elements.
- Set A has the element 10 which is not present in Set B.
Conclusion: Since the sets do not contain the same elements, we can conclude that A≠B.
Summary of Results
- (i) A=B
- (ii) A≠B
- (iii) A≠B
Given:
- A={a,b,c,d}
- B={d,c,b,a}
- Set A contains: a,b,c,d
- Set B contains: d,c,b,a
- Both sets contain the elements a,b,c,d.
Given:
- A={4,8,12,16}
- B={8,4,16,18}
- Set A contains: 4,8,12,16
- Set B contains: 8,4,16,18
- Set A has the element 12 which is not present in Set B.
- Set B has the element 18 which is not present in Set A.
Given:
- A={2,4,6,8,10}
- B={x:x is a positive even integer and x<10}
- The positive even integers less than 10 are: 2,4,6,8.
- Set A contains: 2,4,6,8,10
- Set B contains: 2,4,6,8
- Set A has the element 10 which is not present in Set B.
- (i) A=B
- (ii) A≠B
- (iii) A≠B
Topper's Solved these Questions
- SETSBOOK - NCERTCHAPTER - SETSEXERCISE - SOLVED EXAMPLES
30 Videos
- SETSBOOK - NCERTCHAPTER - SETSEXERCISE - EXERCISE 1.6
7 Videos
- SETSBOOK - NCERTCHAPTER - SETSEXERCISE - EXERCISE 1.3
8 Videos
- SEQUENCES AND SERIESBOOK - NCERTCHAPTER - SEQUENCES AND SERIESEXERCISE - EXERCISE 9.5
6 Videos
- STATISTICSBOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 15.2
10 Videos
Similar Questions
In the following , state whether A=B or not :
(i) A = {a,b,c,d}, B= {d,c,b,a}
(ii) A= {4,8,12,16},B= {8,4,16,18}.
(iii) A={2,4,6,8,10},
B=x:x is a positive even integer and x≤10}
(iv) A= {x:x is multiple of 10},
B= {10,15,20,25,30,.....}.
View SolutionIn the following, state whether A = B or not :
(i) A={a,b,c,d}
(ii) B={d,c,b,a}
(iii) A={2,4,6,8,10}
B = {x : x is positive even integer and x≤10}
(iv) A = {x : x is a multiple of 10}
B={10,15,20,25,30,...}.
View Solution
Knowledge Check
A={x:2<x<8 and x∈N} and B={x:3<x<9 and x∈W}. Find (A−B)∩(B−A).
the following are the steps involved n solving the above problem. Arrange them in sequential order.
(A) A={3,4,5,6,7} and B={4,5,6,7,8}
(B) A−B={3},B−A={8}
(C) A−B={3,4,5,6,7}−{4,5,6,7,8},B−A={4,5,6,7,8}−{3,4,5,6,7}
(D) (A−B)∩(B−A)=ϕAABCDBACBDCABDCDCABD
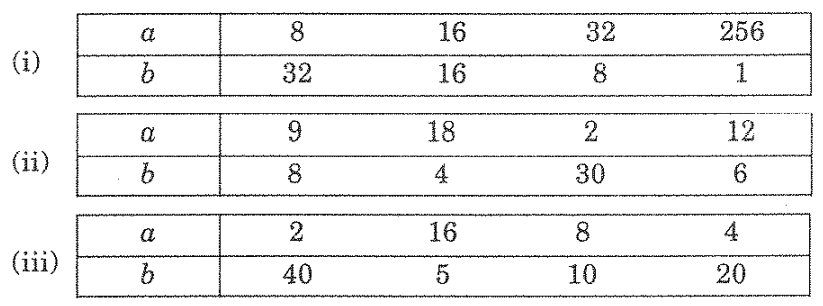
In which of the following tables a and b vary inversely:
View SolutionFind the value of b2−4ac, if
(i) a=3,b=9,c=6 (ii) a=2,b=−8,c=8
(iii) a=1,b=1,c=1.
View SolutionIn Fig. 4.60, check whether AD is the bisector of ∠A of ABC in each of the following: (FIGURE) AB=5cm, AC=10cm, BD=1.5cm and CD=3.5cm (ii) AB=4cm, AC=6cm, BD=1.6cm and CD=2.4cm (iii) AB=8cm, AC=24cm, BD=6cm and BC=24cm
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=4 , AE=8 , DB=x−4 , and EC=3x−19 , find x (ii) If AD=8 cm , AB=12cm and AE=12 cm , find CE . (iii) If AD=4 cm , DB=4.5 cm and AE=8 cm , find AC .
View SolutionWrite the following sets in Set - Builder Form :
(a) (i) A={0}
(ii) B={-1,1}
(iii) C={1,3,5,7,9}
(iv) D={2,4,6,8}
(v) E={1,5,10,15,……}
(vi) F= {12,18,24,…,96}.
(b) (i) ,6,9,12}
(iii) {2,4,8,16,32}
(iii) {5,25,125,625}
(iv) {2,4,6,....}
(v) {1,4,9,.....100}
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=12 cm, AD=8 cm, AE=12 cm and AC=18 cm . (ii) AB=5.6 cm, AD=1.4 cm, AC=7.2 cm and AE=1.8 cm
View SolutionIf A={3,6,9,12,15,18,21}, B={4,8,12,16,20},C={2,4,6,8,10,12,14,16}, D={5,10,15,20}; find
(i) A−B
(ii) A−C
(iii) A−D
View Solution
