Two cars A and B have masses mAandmB respectively, with mA>mB. Both the cars are moving in the same direction with equal kinetic energy. If equal braking force is applied on both, then before coming to rest
A will cover a greater distance
B will cover a greater distance
both will cover the same distance
distance covered by them will depend on their respective velocities
The correct Answer is:B
To solve the problem, we will analyze the situation step by step, considering the properties of kinetic energy, momentum, and the effects of equal braking forces on two cars with different masses.
1. Understanding the Given Information:
- We have two cars, A and B, with masses mA and mB respectively, where mA>mB.
- Both cars are moving in the same direction and have equal kinetic energy.
2. Kinetic Energy Relation:
- The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
- Since both cars have equal kinetic energy, we can write:
KEA=KEB⟹12mAv2A=12mBv2B
- This simplifies to:
mAv2A=mBv2B
3. Momentum Relation:
- The momentum p of an object is given by:
p=mv
- From the kinetic energy relation, we can express the velocities in terms of momentum:
vA=pAmA,vB=pBmB
- Substituting these into the kinetic energy equation gives:
mA(pAmA)2=mB(pBmB)2
- This leads to:
p2AmA=p2BmB
4. Comparing the Momentums:
- Since mA>mB and both kinetic energies are equal, it follows that:
p2A>p2B⟹pA>pB
- Thus, the momentum of car A is greater than that of car B.
5. Applying Equal Braking Force:
- When equal braking forces are applied to both cars, the change in momentum is related to the time taken to stop. The force F is given by:
F=dpdt
- Since the forces are equal, we have:
dpAdt=dpBdt
6. Change in Momentum:
- The change in momentum for both cars is:
ΔpA=pA−0=pA,ΔpB=pB−0=pB
- Since pA>pB, it follows that:
ΔpA>ΔpB
7. Time to Stop:
- From the relation F=dpdt, we can express the time taken to stop:
ΔtA=ΔpAF,ΔtB=ΔpBF
- Since ΔpA>ΔpB and F is constant, it follows that:
ΔtA>ΔtB
8. Distance Travelled Before Coming to Rest:
- The distance travelled while stopping can be found using the equation:
d=viΔt+12a(Δt)2
- Since car A has a higher initial momentum, it will travel a greater distance before coming to rest compared to car B.
Conclusion:
- Car A, with greater mass and momentum, will travel a greater distance before coming to rest than car B, when equal braking forces are applied.
- We have two cars, A and B, with masses mA and mB respectively, where mA>mB.
- Both cars are moving in the same direction and have equal kinetic energy.
- The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
- Since both cars have equal kinetic energy, we can write:
KEA=KEB⟹12mAv2A=12mBv2B
- This simplifies to:
mAv2A=mBv2B
- The momentum p of an object is given by:
p=mv
- From the kinetic energy relation, we can express the velocities in terms of momentum:
vA=pAmA,vB=pBmB
- Substituting these into the kinetic energy equation gives:
mA(pAmA)2=mB(pBmB)2
- This leads to:
p2AmA=p2BmB
- Since mA>mB and both kinetic energies are equal, it follows that:
p2A>p2B⟹pA>pB
- Thus, the momentum of car A is greater than that of car B.
- When equal braking forces are applied to both cars, the change in momentum is related to the time taken to stop. The force F is given by:
F=dpdt
- Since the forces are equal, we have:
dpAdt=dpBdt
- The change in momentum for both cars is:
ΔpA=pA−0=pA,ΔpB=pB−0=pB
- Since pA>pB, it follows that:
ΔpA>ΔpB
- From the relation F=dpdt, we can express the time taken to stop:
ΔtA=ΔpAF,ΔtB=ΔpBF
- Since ΔpA>ΔpB and F is constant, it follows that:
ΔtA>ΔtB
- The distance travelled while stopping can be found using the equation:
d=viΔt+12a(Δt)2
- Since car A has a higher initial momentum, it will travel a greater distance before coming to rest compared to car B.
- Car A, with greater mass and momentum, will travel a greater distance before coming to rest than car B, when equal braking forces are applied.
Topper's Solved these Questions
Similar Questions
Two bodies of unequal mass are moving in the same direction with equal kinetic energy. The two bodies are brought to rest by applying retarding force of same magnitude. How would the distance moved by them before coming to rest compare ?
View SolutionCars I and II, having masses m and 2m respectively, are moving with velocities
2v and v respectively. They are brought to rest by the application of breaks. The cars take the same time and cover the same distance before coming to rest.
What is the ratio of change in kinetic energy of car I to that of car II ?
View Solution
Knowledge Check
Two bodies of masses M and 4M are moving with equal kinetic energy. The ratio of their linear momenta is
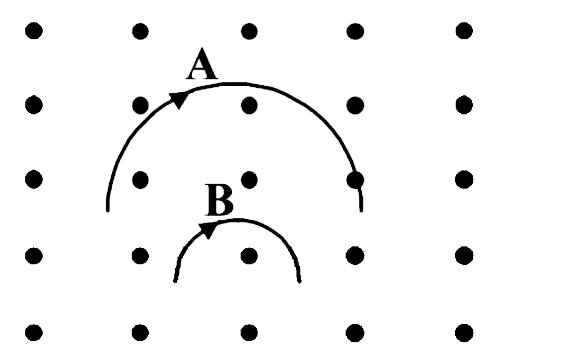
A1:8B1:4C1:2D4:1Two particle A and B of masses mA and mB respectively and having the same charge are moving in a plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are vA and vB respectively and the trajectories are as shown in the figure. Then-
 AmAvA<mBvBBmAvA>mBvBCmA<mBandvA<vBDmA=mBandvA=vB
AmAvA<mBvBBmAvA>mBvBCmA<mBandvA<vBDmA=mBandvA=vBTwo blocks A and B have masses m and 4m, respectively. Each one is acted upon by a force F. If they acquire the same kinetic energy in time tA and tB, then (tA)/(tB) is
A2B12C3D13
Two particles AandB of masses mAandmB respectively and having the same charge are moving in a plane . The speeds of the particles are vAandvB respectively and the trajectories are as shown in the figure. Then
View SolutionThe solid rubber balls A and B having masses 200 and 400 gm respectively are moving in opposite directions with velocity of A equal to 0.3 m / s . After collision the two balls come to rest, then the velocity of B is
View SolutionThe solid rubber balls A and B having masses 200 and 400 gm respectively are moving in opposite directions with velocity of A equal to 0.3 m / s . After collision the two balls come to rest, then the velocity of B is
View SolutionTwo bodies AandB have masses Mandm respectively where M>m and they are at a distance d apart. Equal force is applied to each of them so that they approach each other. The position where they hit each other is :
View SolutionA truck and a car are moving with equal velocity. On applying the brakes both will stop after certain distance, then
View Solution

