Two bodies AandB have masses Mandm respectively where M>m and they are at a distance d apart. Equal force is applied to each of them so that they approach each other. The position where they hit each other is :
nearer to B
nearer to A
at equal distance from AandB
cannot be decided
The correct Answer is:B
(b) Here forces applied should be on opposite directions. So net forces is zero. Their centre of mass wil remain at rest and finally they will meet at centre of mass. And centre of mass lies closer to M.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Displacement , Velocity And Acceleration Of Centre Of Mass
30 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Moment Of Inertia
39 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test
30 Videos
Similar Questions
Two bodies A and B having masses M and 3M respectively are kept at a distance 2.73 m apart. A small particle of mass m is to be place so that the net gravitational force on it, due to A and B is zero. What will be its distance from body A ?
View SolutionTwo particles A and B having masses M and 4M respectively are kept at a distance 2.73 m apart. Another small particle of mass m is to be placed so that the net gravitational force on it is zero. What will be its distance from body A ?
View Solution
Knowledge Check
Two bodies of masses m and M are placed at distance d apart. The gravitational potential (V) at the position where the gravitational field due to them is zero V is
AV=−Gd(m+M)BV=−GdCV=−GMdDV=−Gd√√m+√M2Two particles of mass M and 2M are at a distance D apart. Under their mutual force of attraction they start moving towards each other. The acceleration of their centre of mass when they are D/2 apart is :
A2GM/D2B4GM/D2C8GM/D2DZeroTwo bodies of masses m and 2m are kept at distance r apart from each other. Then the value of G varies as
Ar2Br4Cr−2Drth
Two spheres of masses 2M and M are initially at rest at a distance R apart. Due to mutual force of attraction, they approach each other. When they are at separation R/2, the acceleration of the centre of mass of spheres would be
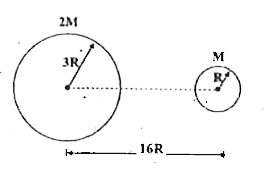
View SolutionTwo spherical bodies of masses 2M and M and radii 3R and R respectively are held at a distance 16R from each other in free space. When they are released they start approaching each other due to the gravitational force of attraction , then find
(a) the ratio of their accelerations during their motion
(b) their velocitites at the time of impact.
View SolutionTwo current elements are placed a certain distance apart but not parallel to each other. Do they exert equal and opposite forces on each other?
View SolutionTwo bodies A and B having masses 2 kg and 4 kg respectively are separated by 2 m. Where should a body of mass 1 kg be placed so that the gravitational force on this body due to bodies A and B is zero?
View SolutionTwo bodies of equal masses attract each other with a force 6.67×10−11N, when placed at a distance 1m apart. The mass of each body is
View Solution
