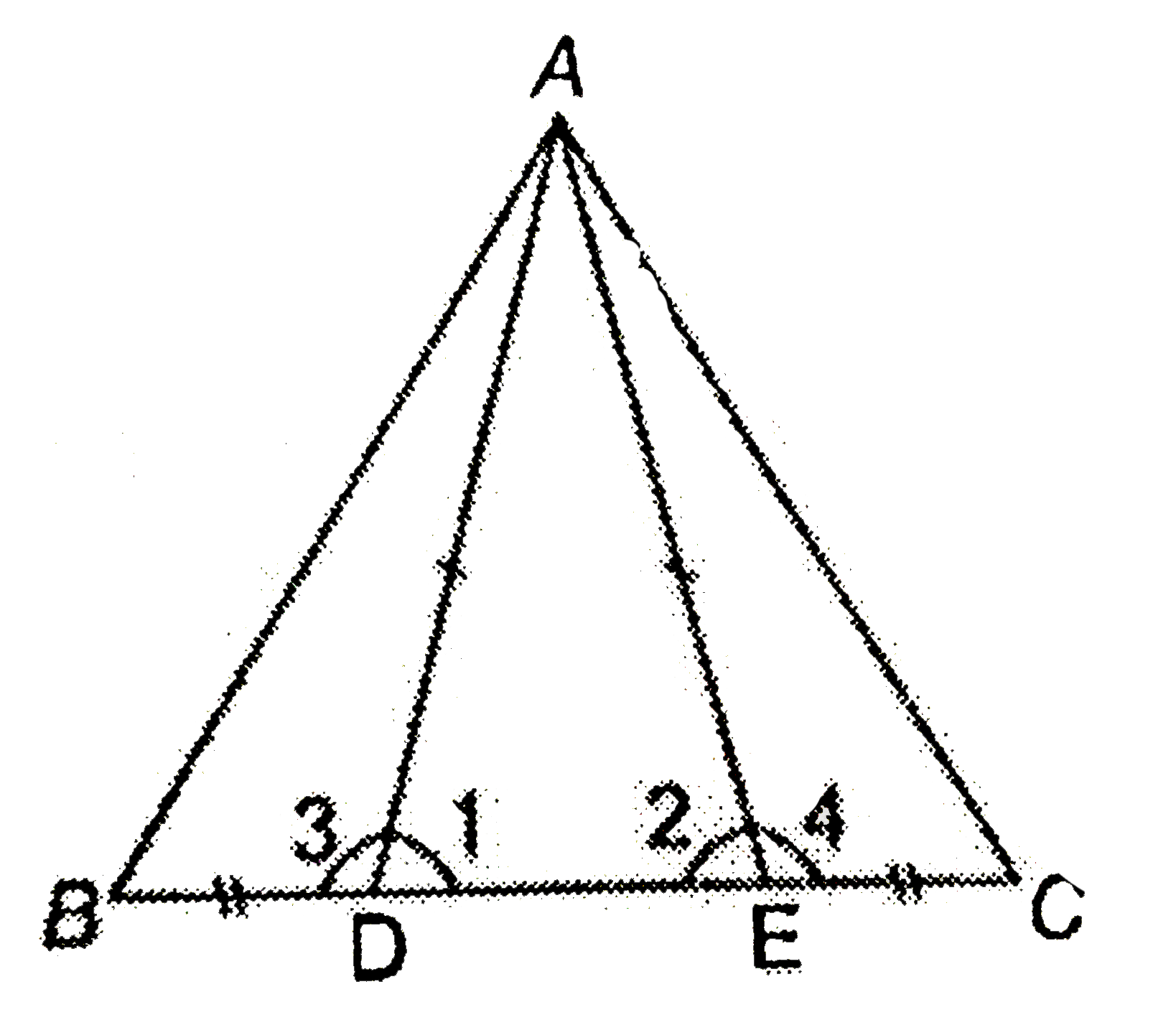
In the given figure, the bisectors of ∠Band∠C of ΔABC meet at I. If IP⊥BC,IQ⊥CA and IR⊥AB, prove that (i) IP=IQ=IR, (ii) IA bisects ∠A.
GIVEN A ΔABC in which BI and CI are the bisectors of ∠Band∠C respectively. IP⊥BC,IQ⊥CAandIR⊥AB.
TO PROVE (i) IP=IQ=IRand(ii)IA bisects ∠A.
PROOF (i) In ΔIPCandΔIQC, we have
∠IPC=∠IQC=90∘ (given)
∠ICP=∠ICQ [∵CI is the bisector of ∠C]
CI=CI (common)
∴ ΔIPC≅ΔIQC (AAS-criteria).
∴ IP=IQ (c.p.c.t.).
Similarly, IQ = IR.
Hence, IP = IQ = IR.
(ii) In ΔIQAandΔIRA, we have
IQ=IR [proved in (i)]
∠IQA=∠IRA [each =90∘]
hyp. IA = hyp. IA (common)
∴ ΔIQA≅ΔIRA (RHS-criteria).
∴ ∠IAQ=∠IAR (c.p.c.t.).
Hence, IA bisects ∠A.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Exercise 9A
Explore 27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Exercise 9B
Explore 16 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:MULTIPLE CHOICE QUESTION(MCQ)
Explore 37 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Multiple Choice Questions (Mcq)
Explore 22 Videos
Similar Questions
Knowledge Check
The internal bisectors of ∠Band∠C of ΔABC meet at O. If ∠A=80∘ then ∠BOC is :
A50∘B160∘C100∘D130∘In △ABC the bisectors of ∠B and ∠C intersect at I if ∠A=70∘ then ∠BIC=…………..
A35∘B75∘C100∘D125∘In the adjacent figure, the bisectors of ∠Aand∠B meet in a point P. If ∠C=100∘and∠D=60∘, find the measure of ∠APB.
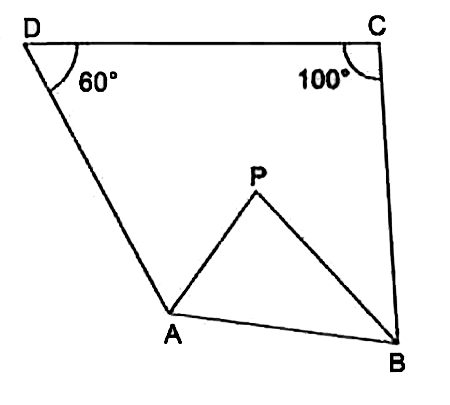 A80∘B100∘C70∘D60∘
A80∘B100∘C70∘D60∘
In the figure, bisectors of ∠Band∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=1/2(∠ABC+∠ADC)
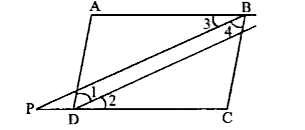
Given: In the given figure, bisectors of ∠Band∠D of a quadrilateral ABCD meet CD and AB produced at P and Q respectively.
To prove: ∠P+∠Q=12(∠ABC+∠ADC)
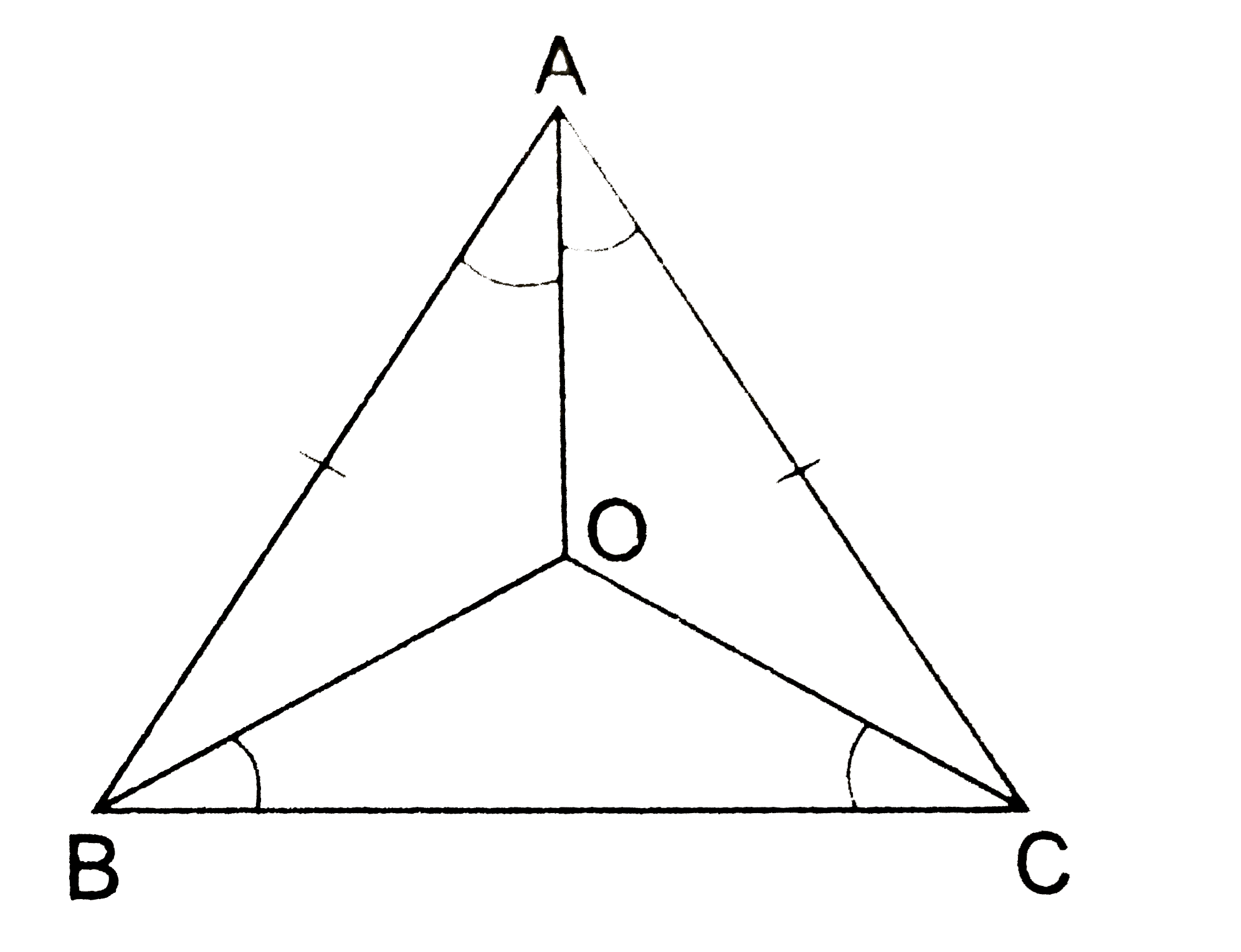
View SolutionIn ΔABC,AB=AC and the bisectors of ∠Band∠C meet at a point O. Prove that BO = CO and the ray AO is the bisector of ∠A.
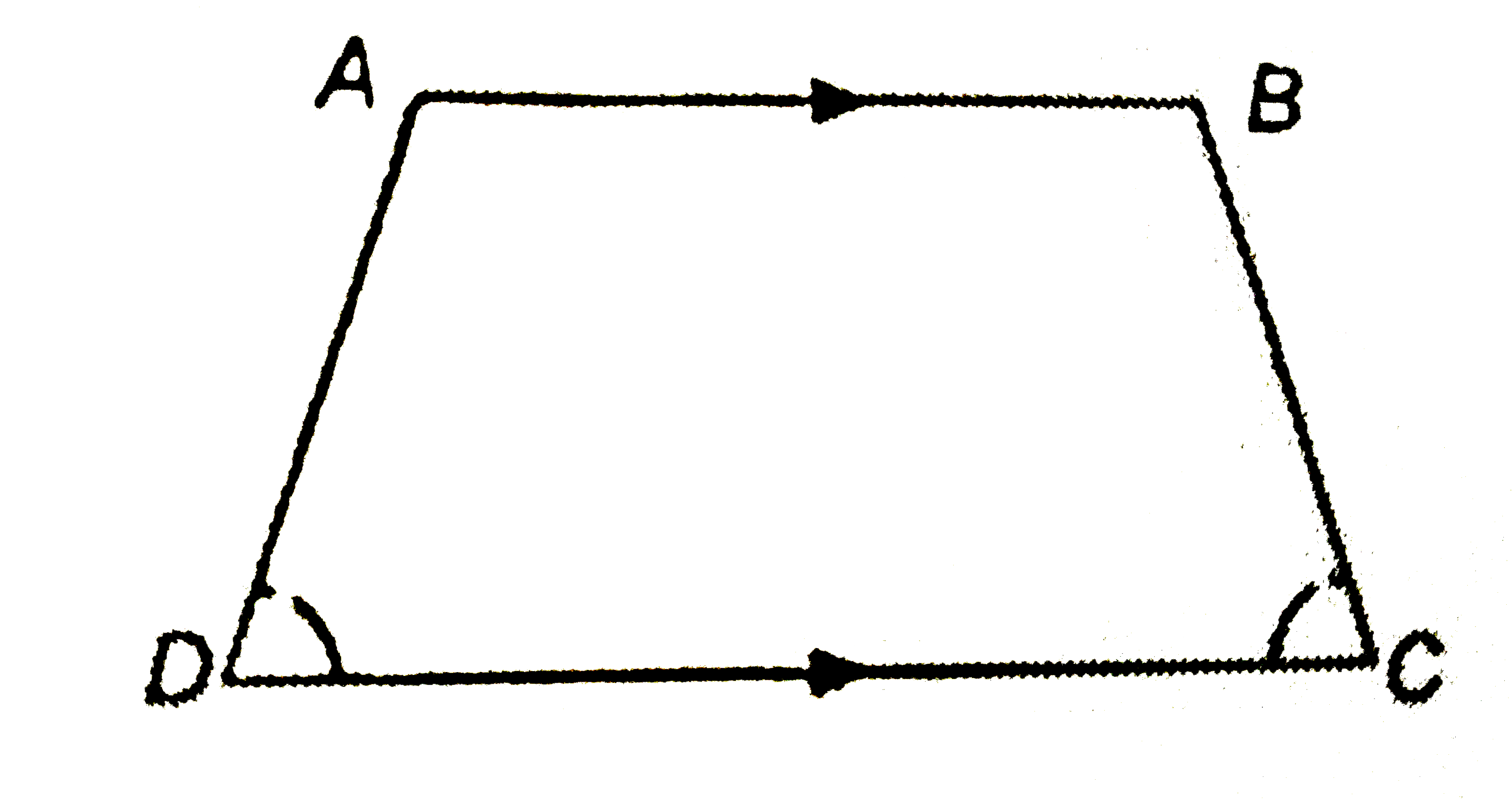
View SolutionIn the given figure, AB||DC and ∠D=∠C. Prove that :
(i) AD=BC
(ii) AC=BD
View SolutionIn the given figure, D and E are the points on the base BC of ΔABC such that BD=CE,AD=AE and ∠ADE=∠AED, prove that ΔADB≅ΔAEC.
View SolutionIn △ABC,∠A=40∘ if bisector of ∠B and ∠C meets at O then prove that ∠BOC=110∘
View Solution
